Tips for using the Doppler effect generalized formula

The Doppler effect generalized formula (Eq. 1) is used to calculate the frequency of a sound wave emitted from a moving source as heard by an observer at a distance from the source, who is also in motion.

$\texrm{(1)}\hspace{40px}\displaystyle{f_o = f_s\left(\frac{v \pm v_o}{v \pm v_s}\right)}$

In Eq. 1, $f_s$ is the frequency emitted by the source, $f_o$ is the frequency heard by an observer from a distance, $v$ is the speed of sound, $v_o$ is the speed of the observer, and $v_s$ is the speed of the source.

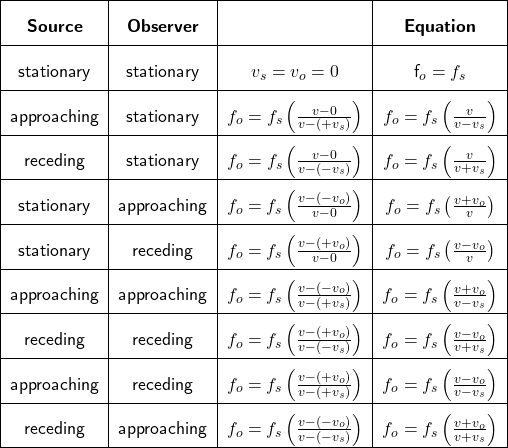
The equation is a combined form of nine separate equations derived for nine scenarios:

Both the source and observer are stationary, resulting in no Doppler effect. The sound frequency heard by the observer is the same as the frequency emitted from the source.
The source approaches a stationary observer.
The source recedes from a stationary observer.
The observer approaches a stationary source.
The observer recedes from a stationary source.
Both the source and observer approach each other.
Both the source and the observer move away from each other.
The source approaches an observer who is moving away from the source.
The observer approaches a source that is moving away.

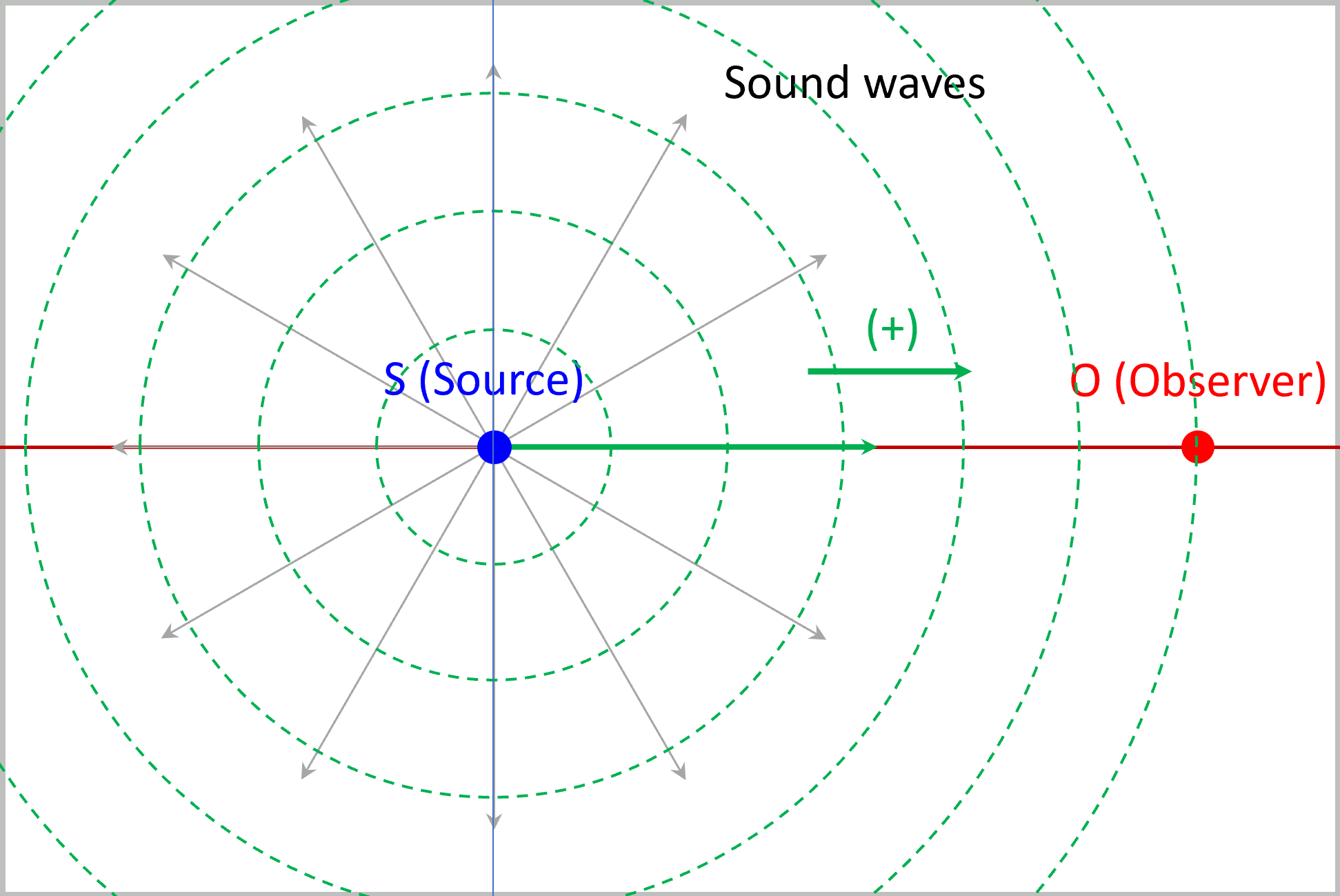
These equations are derived under the conditions that the source frequency is constant, and the speeds of both the source and observer are also constant. Additionally, the motion of the source and observer must be along a straight line joining them (see Figure 1). Note that while sound waves spread out from the source in all directions, only the direction from the source to the observer is considered in these calculations, resulting in a one-dimensional motion axis for sound, source, and observer.

(Derivation of these equations can be found h ere.)

**Figure 1:** Sound waves from a source traveling to an observer located at a distance from the source.

Identifying a Doppler effect equation for a specific scenario using the generalized Doppler effect formula can be confusing, but there is a simple way to make the task easier by noting that the ratio on the right-hand side of the generalized formula (Eq. 1) represents the relative speed of the sound wave and the observer over the relative speed of the sound wave and the source along their traveling axis. Using the concept of relative speed, Eq. 1 can be rewritten as:

$\texrm{(2)}\hspace{40px}\displaystyle{f_o = f_s\left(\frac{|\vec{v}| - |\vec{v}_{o}|}{|\vec{v}| - |\vec{v}_{s}|}\right)}$

where $\vec{v}$ and $|\vec{v}|$ , $\vec{v}_{o}$ and $|\vec{v}_{o}|$ , $\vec{v}_{s}$ and $|\vec{v}_{s}|$ , are the velocities and speeds of sound, observer, and source, respectively.

For one dimensional motion, as in this case, for a vector $\vec{x}$ , if $x$ is its magnitude, then $|\vec{x}|$ is defined as follows:

$\texrm{(3)}\hspace{40px}\displaystyle{|\vec{x}| = \begin{cases} x & \text{if $\vec{x}$ points to the positive direction} \\ -x & \text{if $\vec{x}$ points to the negative direction} \end{cases} }$

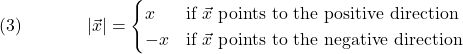
Applying this definition (Eq. 3) to the speeds of sound, observer, and source in Eq. 2, the Doppler effect equation for each of the nine scenarios can be easily extracted from the generalized Doppler effect formula as shown in Table 1. Figure 2 can be utilized to visualize the sign (positive or negative) of the speed of interest. It’s worth noting that the selection of a positive direction for reference will not impact the final results. The same Doppler effect equation will be obtained even if the reference positive direction points in the opposite direction.

**Figure 2**: Sign (positive or negative) of the source’s and the observer’s speeds relative to the (+) direction.

$\textbf{Table 1:}$ Doppler effect equation for each of the nine scenarios
$\renewcommand{\arraystretch}{2.0} \textsf{ \begin{center} \begin{tabular}{ | c | c | c | c | } \hline $\textbf{Source}$ & $\textbf{Observer}$ & & $\textbf{Equation}$\\ \hline stationery& stationery& $v_s = v_o = 0$& f_o = f_s \\ \hline approaching& stationery& $f_o = f_s\left(\frac{v - 0}{v - (+v_s)}\right)$& $f_o = f_s\left(\frac{v}{v - v_s}\right)$ \\ \hline receding& stationery& $f_o = f_s\left(\frac{v - 0}{v - (-v_s)}\right)$& $f_o = f_s\left(\frac{v}{v + v_s}\right)$ \\ \hline stationery& approaching& $f_o = f_s\left(\frac{v - (-v_o)}{v - 0}\right)$& $f_o = f_s\left(\frac{v + v_o}{v}\right)$ \\ \hline stationery& receding& $f_o = f_s\left(\frac{v - (+v_o)}{v - 0}\right)$& $f_o = f_s\left(\frac{v - v_o}{v}\right)$ \\ \hline approaching& approaching& $f_o = f_s\left(\frac{v - (-v_o)}{v - (+v_s)}\right)$& $f_o = f_s\left(\frac{v + v_o}{v - v_s}\right)$ \\ \hline receding& receding& $f_o = f_s\left(\frac{v - (+v_o)}{v - (-v_s)}\right)$& $f_o = f_s\left(\frac{v - v_o}{v + v_s}\right)$ \\ \hline approaching& receding& $f_o = f_s\left(\frac{v - (+v_o)}{v - (+v_s)}\right)$& $f_o = f_s\left(\frac{v - v_o}{v - v_s}\right)$ \\ \hline receding& approaching& $f_o = f_s\left(\frac{v - (-v_o)}{v - (-v_s)}\right)$& $f_o = f_s\left(\frac{v + v_o}{v + v_s}\right)$ \\ \hline \end{tabular} \end{center} }$