Two dimensional Collisions
PROBLEM:
A 1000 kg car traveling north-east at speed 20 m/s collides with a 1800 kg car traveling west at speed 16 m/s. After the collision the two cars stick together and skid for a distance. Calculate the speed and direction of the wreckage immediately after the collision. Is it an elastic or inelastic collision?
SOLVE:
Figure 1 depicts the described collision, where direction west – east is ![]() -axis, south – north is
-axis, south – north is ![]() -axis. South-west – north-east direction forms an angle of
-axis. South-west – north-east direction forms an angle of ![]() with
with ![]() -axis. This is a two-dimensional (2D) event as it has components in both
-axis. This is a two-dimensional (2D) event as it has components in both ![]() and
and ![]() directions.
directions.
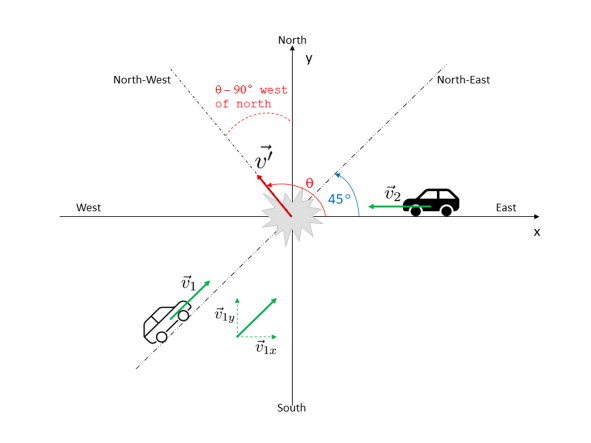
Figure 1
Let ![]() and
and ![]() and
and ![]() and
and ![]() be the masses and velocities of car 1 and car 2, then
be the masses and velocities of car 1 and car 2, then ![]() 1000 kg,
1000 kg, ![]() 1800 kg, speed
1800 kg, speed ![]() 20 m/s and speed
20 m/s and speed ![]() 16 m/s.
16 m/s.
If we only consider the interaction between car 1 and car 2, and ignore all surrounding factors, such as the friction between the cars and the road surface, then this is an isolated system. The total linear momentum of an isolated system must be conserved, therefore, if ![]() and
and ![]() are total linear momenta of the system before and after the collision, respectively, then
are total linear momenta of the system before and after the collision, respectively, then
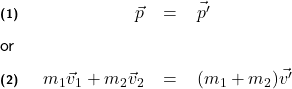
where ![]() is the velocity of the wreckage immediately after the collision (whose
is the velocity of the wreckage immediately after the collision (whose ![]() and
and ![]() components are
components are ![]() and
and ![]() , respectively). Note that
, respectively). Note that
![]()
![]() =
= ![]()
As this is a 2D collision, the total linear momentum of the system must be conserved in both ![]() and
and ![]() directions separately, thus,
directions separately, thus,
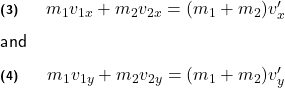
From Figure 1, it can be seen that ![]() and
and ![]() (the
(the ![]() and
and ![]() components of velocity
components of velocity ![]() ) have values of
) have values of

Similarly, values of ![]() and
and ![]() components of velocity
components of velocity ![]() can be calculated
can be calculated
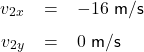
Re-arranging equations (3) and (4), ![]() and
and ![]() can be obtained as follows
can be obtained as follows
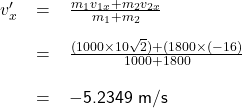
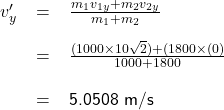
As a result, the speed of the wreckage right after the collision is
![]() 7.2743 m/s
7.2743 m/s
Direction of the wreckage can be determined by the angle ![]() , formed by
, formed by ![]() with the
with the ![]() -axis.
-axis.
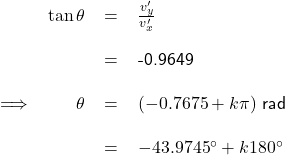
where ![]()
Based on the values of ![]() and
and ![]() , it can be deduced that
, it can be deduced that ![]() = 1, hence
= 1, hence ![]() -43.9745
-43.9745![]() + 180
+ 180![]() 136.0255
136.0255![]() or 46.0255
or 46.0255![]() to the west of the north axis.
to the west of the north axis.
To determine whether a collision is elastic or inelastic, we consider the total kinetic energy of the system. A collision is elastic if there is no loss in the system’s kinetic energy after the collision.
Let ![]() and
and ![]() be the kinetic energy of the system before and after the collision, respectively, then
be the kinetic energy of the system before and after the collision, respectively, then
Kinetic energy of the system before the collision:
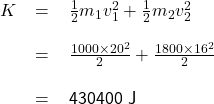
Kinetic energy of the system after collision:
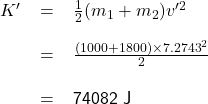
As ![]() ≠
≠ ![]() , this is an inelastic collision.
, this is an inelastic collision.
Note that a collision in which the involved objects stick together and move with a common final velocity is termed perfectly inelastic collision. In this type of collision, the maximum amount of energy is lost from the system’s kinetic energy. Also note that, the total energy of the system is conserved, as kinetic energy of the system is only transformed into internal energy (cars’ deformation) and heat after the collision.
