Number Systems

Part 2: Decimal numbers to other number systems

Decimal numbers and other number systems and how to convert a number in any number system to a decimal value are explained in Number S ystems, Part 1. In this page, Part 2 of Number Systems, we will discuss how to convert decimal numbers to other number systems.

A. Decimal numbers to binary numbers

If you want to find the value of a decimal number, say the number 13, in the binary system, you would want to find a way to express the number 13 in a format that looks like the left hand side of Eqs. (B.1) or (B.2) in Nu mber Systems, Part 1. We will explore that process as follows

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} 13 &= &(6\times\textcolor{blue}{2}) + \textcolor{red}{1} \\ &= &(3\times\textcolor{blue}{2})\times\textcolor{blue}{2} + \textcolor{red}{1} \\ &= &(2 + 1)\times\textcolor{blue}{2}^2 + \textcolor{red}{1} \\ &= &\textcolor{blue}{2}^{3} + (\textcolor{red}{1} \times\textcolor{blue}{2}^2) + \textcolor{red}{1} \\ &= &\textcolor{red}{1}\times\textcolor{blue}{2}^{3} + \textcolor{red}{1}\times\textcolor{blue}{2}^{2} + \textcolor{red}{1}\times\textcolor{blue}{2}^{0} \end{tabular} }$

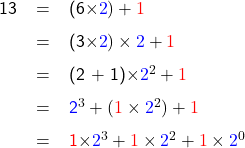
Filling the missing term 2¹ with zero (0), we have

$\textsf{\textbf{\small{Eq. A.1:}}}$
$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} 13 &= (\textcolor{red}{1}\times\textcolor{blue}{2}^3) + (\textcolor{red}{1} \times\textcolor{blue}{2}^2) + (\textcolor{red}{0}\times\textcolor{blue}{2}^1) + (\textcolor{red}{1}\times\textcolor{blue}{2}^0) \end{tabular} }$

$\textsf{ \implies \boxed{(13)_{\textcolor{blue}{10}} = (1101)_{\textcolor{blue}{2}}} }$

These above calculation steps can be described by a general expression of $Dividend = Quotient \times Divisor + Remainder$
(e.g., $13 = 6\times2+1$ ) , and can be re-arranged and tabulated as shown in Table A.1.

$\textbf{Table A.1:}$ Conversion of decimal number 13 to binary number
$\begin{center} \begin{tabular}{ | r c l | c | r | l|} \hline Dividend &\div &Divisor (Base) & Quotient & \textcolor{red}{Remainder} & Term\\ \hline 13 &\div & \textcolor{blue}{2} & 6 & \textcolor{red}{1} & 2^0 \\ \hline 6 &\div & \textcolor{blue}{2} & 3 & \textcolor{red}{0} & 2^1 \\ \hline 3 &\div & \textcolor{blue}{2} & 1 & \textcolor{red}{1} & 2^2 \\ \hline 1 &\div & \textcolor{blue}{2} & 0 & \textcolor{red}{1} & 2^3 \\ \hline \end{tabular} \end{center}$

Note that the last two columns in Table A.1 can be used to form Eq. A.1 and hence the binary number of interest (1101). Subsequently, we can derive calculating steps for converting a decimal number to binary number as follows:

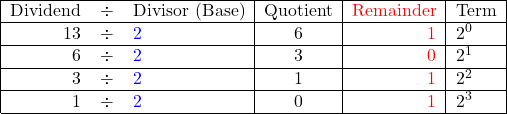
(i): First, divide the number (13 in this demo) by the new base, which is 2. The remainder of this division is the first digit of the binary number, start from right to left, while the quotient becomes the dividend of the next step.
(ii): Next, divide the new dividend by the base, the remainder of this division is the second digit added to the left of the digit obtained in step (i), and so on.
(iii): The calculation stops when the quotient is equal to zero.

To convert a decimal number that has a fractional part, for example 13.325, to a binary number, first take notice that 13.325 = 13 + 0.325. The conversion of decimal number 13 to binary number is described in the previous section. The following section will explain how to convert fractional decimal number 0.325 to binary.

First take notice that 0.325 can be represented as the following (see Eq. B.2 in Number Systems – Part 1)

$\textsf{\textbf{\small{Eq. A.2:}}}$
$\textsf{ (0.325)_{10} = (\textcolor{red}{x_1}\times\textcolor{blue}{2}^{-1}) + (\textcolor{red}{x_2}\times\textcolor{blue}{2}^{-2}) + (\textcolor{red}{x_3}\times\textcolor{blue}{2}^{-3}) + \quad \dots }$

where x₁, x₂, x₃ (highlighted in red) are the unknown digits we want to determine, and Eq. A.2 means

$\textsf{ (0.325)_{10} = (\textcolor{red}{x_1}\times\frac{1}{2}) + (\textcolor{red}{x_2}\times\frac{1}{4}) + (\textcolor{red}{x_3}\times\frac{1}{8}) + \quad \dots }$

$\textsf{ (0.325)_{10} = (\textcolor{red}{x_1}\times 0.5) + (\textcolor{red}{x_2}\times 0.25}) + (\textcolor{red}{x_3}\times 0.125) + \quad \dots }$

There are various ways to find x₁, x₂, x₃, but here we will again use the concept of division’s quotient and remainder, but first take notice that

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} 0.325 &= &(0\times\textcolor{blue}{0.50}) + \textcolor{red}{0.325} \\ \textcolor{red}{0.325}&= &(1\times\textcolor{blue}{0.25}) + \textcolor{green}{0.125} \\ \textcolor{green}{0.125} &= &(1\times\textcolor{blue}{0.125}) + 0 \end{tabular} }$

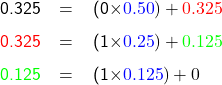
which implies

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} 0.325 &= &(0\times\textcolor{blue}{0.50}) + (1\times\textcolor{blue}{0.25}) + (1\times\textcolor{blue}{0.125}) \end{tabular} }$

$\textsf{\textbf{\small{Eq. A.3:}}}$
$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} 0.325 &= &(\textcolor{red}{0}\times\textcolor{blue}{2}^{-1}) + (\textcolor{red}{1}\times\textcolor{blue}{2}^{-2}) + (\textcolor{red}{1}\times\textcolor{blue}{2}^{-3}) \end{tabular} }$

$\textsf{ \implies \boxed{(0.325)_{\textcolor{blue}{10}} = (.011)_{\textcolor{blue}{2}}} }$

(Hence, $x_1$ = 0, $x_2$ = 1, and $x_1$ = 1)

Combining Eqs. A.1 and A.3, we have

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (13.325)_{\textcolor{blue}{10}} &= &(13)_{\textcolor{blue}{10}} + (0.325)_{\textcolor{blue}{10}} \\ &= &(1101)_{\textcolor{blue}{2}} + (.011)_{\textcolor{blue}{2}} \end{tabular} }$

$\textsf{ \implies \boxed{(13.325)_{\textcolor{blue}{10}} = (1101.011)_{\textcolor{blue}{2}}} }$

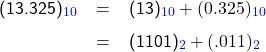
A table similar to Table A.1 can be constructed for converting steps for number 0.325, but this time the remainder of the division is used as the dividend for the next step, while the quotient becomes a digit of the new number.

$\textbf{Table A.2:}$ Conversion of decimal fractional number 0.325 to binary number
$\textsf{ \begin{center} \begin{tabular}{ | r c l | c | r | l|} \hline Dividend &\div &Divisor & \textcolor{red}{Quotient} & Remainder & Term\\ \hline 0.325 &\div & \textcolor{blue}{0.50} & \textcolor{red}{0} & 0.325 & {\textcolor{blue}{2}}^{\textcolor{blue}{-1}} \\ \hline 0.325 &\div & \textcolor{blue}{0.25} & \textcolor{red}{1} & 0.125 & {\textcolor{blue}{2}}^{\textcolor{blue}{-2}} \\ \hline 0.125 &\div & \textcolor{blue}{0.125} & \textcolor{red}{1} & 0 & {\textcolor{blue}{2}}^{\textcolor{blue}{-3}} \\ \hline \end{tabular} \end{center} }$

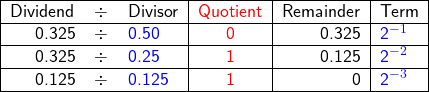
Notes that in this conversion, the divisors are the decimal values of their corresponding terms, i.e., 0.50 = 2^-1, 0.25 = 2^-2, and so on.

From Table A.2, it can be seen that the steps for converting a decimal fractional number to binary number are as follows

(i): Divide the number (0.325 in this case) by the first term after the fractional point, which is 2^-1 (0.5). Unlike conversion of the whole number, for the fractional part, the quotient of this division is the first digit of the binary part after the fractional point, starting from left to right, while the remainder becomes the dividend for the next step.
(ii): Divide the new dividend by the next term of the base, which is 2^-2 (0.25), the quotient of this division will be the second digit, on the right of the digit obtained in step 1, and so on.
(iii): The calculation stops when the remainder is equal to zero or meets a pre-set criterion (see below Note).

Note: In this calculation, both dividend (numerator) and divisor (denominator) are fractional numbers, therefore, the remainder may not always converge to zero. Instead of “Remainder = 0”, a different criterion should be used such as limiting the number of digits after the fractional point, or setting “Remainder < ε ” where ε << 0 (for example, ε = 10^-6) to stop the calculation process.

B. Decimal numbers to Hexadecimal numbers

Conversion of decimal number to hexadecimal number is similar to conversion of decimal number to binary number except that the base is now 16 instead of 2, and the symbols used for representing a hexadecimal number are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, where the values of A, B, C, D, E, F are 10, 11, 12, 13, 14, 15, respectively. For example, let’s convert the decimal number 2590.175 to a hexadecimal number.

Because 2590.175 = 2590 + 0.175, we can first split the number into two parts: the whole number 2590 and the fractional part, 0.175. We then follow the steps described in Table A.1 for the whole number 2590 and steps in Table A.2 for the fractional number 0.175, and then add the two results together to obtain the final result.

Calculation steps for the whole number 2590 are shown in Table B.1, and calculation steps for the fractional part 0.175 are shown in Table B.2.

$\textbf{Table B.1:}$ Conversion of decimal number 2590 to hexadecimal number
$\begin{center} \begin{tabular}{ | r c l | c | r | l|} \hline Dividend &\div &Divisor (Base) & Quotient & \textcolor{red}{Remainder} & Term\\ \hline 2590 &\div & 16 & 161 & \textcolor{red}{14} & 16^0 \\ \hline 161 &\div & 16 & 10 & \textcolor{red}{1} & 16^1 \\ \hline 10 &\div & 16 & 0 & \textcolor{red}{10} & 16^2 \\ \hline \end{tabular} \end{center}$
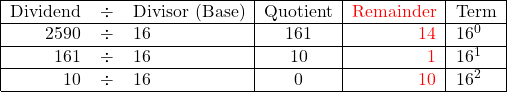
Substitute 10, and 14 with A and E, respectively, decimal number 2590 can be expressed as

$\textsf{\textbf{\small{Eq. B.1:}}}$
$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (2590)_{\textcolor{blue}{10}} &= (\textcolor{red}{A}\times\textcolor{blue}{16}^{2}) + (\textcolor{red}{1}\times\textcolor{blue}{16}^{1}) + (\textcolor{red}{E}\times\textcolor{blue}{16}^{0}) \end{tabular} }$

Therefore, the hexadecimal value of decimal number 2590 is A1E.

$\textbf{Table B.2:}$ Conversion of decimal fractional number 0.175 to hexadecimal number
$\begin{center} \begin{tabular}{ | l c l | c | l | l|} \hline Dividend &\div &Divisor & \textcolor{red}{Quotient} & Remainder & Term\\ \hline 0.175 &\div & 16^{-1} & \textcolor{red}{2} & 0.05 & 16^{-1} \\ \hline 0.05 &\div & 16^{-2} & \textcolor{red}{12} & 3.125\times10^{-3} & 16^{-2} \\ \hline 3.125\times10^{-3} &\div & 16^{-3} & \textcolor{red}{12} & 1.95312\times10^{-4} & 16^{-3} \\ \hline 1.95312\times10^{-4} &\div & 16^{-4} & \textcolor{red}{12} & 1.2207\times10^{-5} & 16^{-4} \\ \hline \end{tabular} \end{center}$
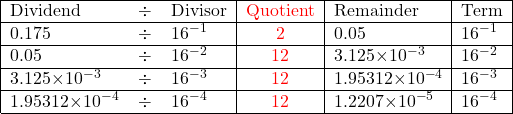
Here, we stop after 4 calculations because the remainder of the division will take many more steps to reach zero, but the calculation could continue if higher level of accuracy is desired.
After substituting 12 with C, 0.175 can be expressed as

$\textsf{\textbf{\small{Eq. B.2:}}}$
$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (0.175)_{\textcolor{blue}{10}} &= (\textcolor{red}{2}\times\textcolor{blue}{16}^{-1}) + (\textcolor{red}{C}\times\textcolor{blue}{16}^{-2}) + (\textcolor{red}{C}\times\textcolor{blue}{16}^{-3}) + (\textcolor{red}{C}\times\textcolor{blue}{16}^{-4})\quad \dots \end{tabular} }$

Therefore, the hexadecimal value for the fractional part 0.175 is .2CCC

Combining Eqs. B.1 and B.2, we have

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (2590.175)_{\textcolor{blue}{10}} &= &(2590)_{\textcolor{blue}{10}} + (0.175)_{\textcolor{blue}{10}} \\ &= &(\textcolor{red}{A}\times\textcolor{blue}{16}^{2}) + (\textcolor{red}{1}\times\textcolor{blue}{16}^{1}) + (\textcolor{red}{E}\times\textcolor{blue}{16}^{0}) + (\textcolor{red}{2}\times\textcolor{blue}{16}^{-1}) + \\ & &(\textcolor{red}{C}\times\textcolor{blue}{16}^{-2}) + (\textcolor{red}{C}\times\textcolor{blue}{16}^{-3}) + (\textcolor{red}{C}\times\textcolor{blue}{16}^{-4}) \quad \dots \end{tabular} }$

$\textsf{ \implies \boxed{(2590.175)_{\textcolor{blue}{10}} = (A1E.2CCC)_{\textcolor{blue}{16}}} }$

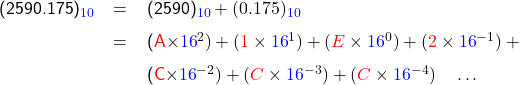
C. Decimal numbers to octal and other systems

To convert a decimal number to an octal number, or, in fact, to any other base system, the same approach described above can be used. For example, let’s convert the decimal number 2590.175 to an octal number (a base-8 number). As 2590.175 = 2590 + 0.175, we will build two tables, Table C.1 for number 2590 and Table C.2 for 0.175, as follows:

$\textbf{Table C.1:}$ Conversion of decimal number 2590 to octal number (base-8)
$\begin{center} \begin{tabular}{ | r c l | c | r | l|} \hline Dividend &\div &Divisor (Base) & Quotient & \textcolor{red}{Remainder} & Term\\ \hline 2590 &\div & 8 & 323 & \textcolor{red}{6} & 8^0 \\ \hline 323 &\div & 8 & 40 & \textcolor{red}{3} & 8^1 \\ \hline 40 &\div & 8 & 5 & \textcolor{red}{0} & 8^2 \\ \hline 5 &\div & 8 & 0 & \textcolor{red}{5} & 8^3 \\ \hline \end{tabular} \end{center}$

Therefore,
$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (2590)_{\textcolor{blue}{10}} &= (\textcolor{red}{5}\times\textcolor{blue}{8}^{3}) + (\textcolor{red}{0}\times\textcolor{blue}{8}^{2}) + (\textcolor{red}{3}\times\textcolor{blue}{8}^{1}) + (\textcolor{red}{6}\times\textcolor{blue}{8}^{0}) \end{tabular} }$

$\textbf{Table C.2:}$ Conversion of decimal fractional number 0.175 to octal number (base-8)
$\begin{center} \begin{tabular}{ | l c l | c | l | l|} \hline Dividend &\div &Divisor & \textcolor{red}{Quotient} & Remainder & Term\\ \hline 0.175 &\div & 8^{-1} & \textcolor{red}{1} & 0.05 & 8^{-1} \\ \hline 0.05 &\div & 8^{-2} & \textcolor{red}{3} & 0.003125 & 8^{-2} \\ \hline 0.003125 &\div & 8^{-3} & \textcolor{red}{1} & 0.001172 & 8^{-3} \\ \hline 0.001172 &\div & 8^{-4} & \textcolor{red}{4} & 0.000195& 8^{-4} \\ \hline \end{tabular} \end{center}$

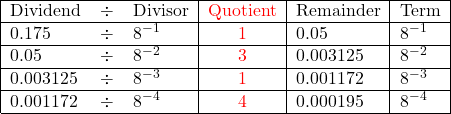
The calculation could continue if a higher level of accuracy is desired, but here we stop at remainder = 0.000195, and the base-8 number of 0.175 is

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (0.175)_{\textcolor{blue}{10}} &= (\textcolor{red}{1}\times\textcolor{blue}{8}^{-1}) + (\textcolor{red}{3}\times\textcolor{blue}{8}^{-2}) + (\textcolor{red}{1}\times\textcolor{blue}{8}^{-3}) + (\textcolor{red}{4}\times\textcolor{blue}{8}^{-4})\quad \dots \end{tabular} }$

Therefore, the octal number of 2590.175 is

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{r c l} (2590.175)_{\textcolor{blue}{10}} &= &(2590)_{\textcolor{blue}{10}} + (0.175)_{\textcolor{blue}{10}} \\ &= &(\textcolor{red}{5}\times\textcolor{blue}{8}^{3}) + (\textcolor{red}{0}\times\textcolor{blue}{8}^{2}) + (\textcolor{red}{3}\times\textcolor{blue}{8}^{1}) + (\textcolor{red}{6}\times\textcolor{blue}{8}^{0}) + (\textcolor{red}{1}\times\textcolor{blue}{8}^{-1}) + \\ & &(\textcolor{red}{3}\times\textcolor{blue}{8}^{-2}) + (\textcolor{red}{1}\times\textcolor{blue}{8}^{-3}) + (\textcolor{red}{4}\times\textcolor{blue}{8}^{-4}) \quad \dots \end{tabular} }$

$\textsf{ \implies \boxed{(2590.175)_{\textcolor{blue}{10}} = (5036.1314)_{\textcolor{blue}{8}}} }$

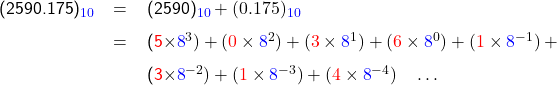
Notes:

The method described above can be used for any other number systems, only that the base needs to be replaced accordingly.
The greater the base is, the more compact the number is
For the fractional part, criterion “Remainder = 0” may be impossible to achieve in many cases, causing the calculations to be infinite. Substituting zero with criterion “Remainder < ε”, where ε is a number close to zero, as seen in the above demo, while not produce the exact value, can overcome the problem. The value of ε can be chosen depending on the level of accuracy required.
If you are dealing with conversion of binary numbers to quaternary (base 4), or octal (base 8), or hexadecimal (base 16) number systems, and vice versa, there is a simple method to convert the number without using division. This approach is described in Number Systems – Part 3
Microsoft Excel functions quotient() and mod() can be used to obtain quotient and remainder of a division, respectively. For those who are interested in computing, a Python code showing how to convert a number of any base to another number system, including decimal system, can be found here. An error tolerance (or ε) of 10×^-6 is used in the code.

Number Systems

Part 2: Decimal numbers to other number systems

A. Decimal numbers to binary numbers

B. Decimal numbers to Hexadecimal numbers

C. Decimal numbers to octal and other systems

Number Systems – Conversion to Decimal system

Number Systems – Part 3: Binary Numbers & Base-4, Base-8, Base-16 Number Systems

Check your number