Number Systems

Number Systems and Their Decimal Equivalents

Number Systems and Their Decimal Equivalents
A. Decimal Number System
B. Binary Number System
C. Hexadecimal Number System
D. Octal Number System
E. Other Number Systems

Related topics
• Decimal Numbers – Conversion to Other Number Systems
• Conversion Between Binary Numbers and Quaternary, Octal, or Hexadecimal Numbers
• Number Conversion Tool

A number system or numbering system is a system that represents numbers in a unique manner using a specific set of symbols. For instance, the decimal system is a number system based on number 10, which is referred to as the base or basis of the system. If n is the base of a number system, then there are n distinct symbols ranging from 0 to n-1 used to represent numbers in that system. Common number systems include decimal (base 10), binary (base 2), hexadecimal (base 16), and octal (base 8).

A. Decimal Number System (Base-10 Number System)

For decimal system, the symbols (or digits) used to represent numbers in the system are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, for example, number 526 or number 526.38.

In the decimal system, number 526 can be expressed as

$\textsf{ \textcolor{red}{526} = (\textcolor{red}{5}\times100) + (\textcolor{red}{2}\times10) + (\textcolor{red}{6}\times1)}$

$\textsf{\textbf{\small{Eq. A.1:}}}$
$\textsf{ \textcolor{red}{526} = (\textcolor{red}{5}\times\textcolor{blue}{10}^2) + (\textcolor{red}{2}\times\textcolor{blue}{10}^1) + (\textcolor{red}{6}\times\textcolor{blue}{10}^0) }$

Note that the meaning and position of each digit (in red) in number 526 are defined by its respective term on the right hand side (RHS) of Eq. (A.1), whereas the base is in blue color.

Similarly, number 526.38 can be expressed as

$\textsf{ \textcolor{red}{526.38} = (\textcolor{red}{5}\times100) + (\textcolor{red}{2}\times10) + (\textcolor{red}{6}\times1) + (\textcolor{red}{3}\times0.1) + (\textcolor{red}{8}\times0.01)}$

$\textsf{\textbf{\small{Eq. A.2:}}}$
$\textsf{ \textcolor{red}{526.38} = (\textcolor{red}{5}\times\textcolor{blue}{10}^2) + (\textcolor{red}{2}\times\textcolor{blue}{10}^1) + (\textcolor{red}{6}\times\textcolor{blue}{10}^0) + (\textcolor{red}{3}\times\textcolor{blue}{10}^{-1}) + (\textcolor{red}{8}\times\textcolor{blue}{10}^{-2}) }$

Again, note that the meaning and position of each digit in number 526.38 are defined by its respective term on the RHS of Eq. (A.2), and also note that digits following the decimal point (i.e., 3, 8) have negative sign in its exponent term on the RHS.

B. Binary Number System (Base-2 Number System)

For binary system, because the base is 2, only digits 0 and 1 can be used to represent the numbers. Numbers 1101 and 1101.01 are two examples of binary numbers. Similar to Eq. (A.1), but with the base is now 2 instead of 10, binary number 1101 can be written as

$\textsf{\textbf{\small{Eq. B.1:}}}$
$\textsf{ \textcolor{red}{1101} = (\textcolor{red}{1}\times\textcolor{blue}{2}^3) + (\textcolor{red}{1}\times\textcolor{blue}{2}^2) + (\textcolor{red}{0}\times\textcolor{blue}{2}^1)+ (\textcolor{red}{1}\times\textcolor{blue}{2}^0)}$

which in decimal system means

$\textsf{ \textcolor{red}{1101} = (\textcolor{red}{1}\times8) + (\textcolor{red}{1}\times4) + (\textcolor{red}{0}\times2) + (\textcolor{red}{1}\times1)}$

$\textsf{ (\textcolor{red}{1101})_{\textcolor{blue}{2}} = 8 + 4 + 1 = (13)_{\textcolor{blue}{10}} }$

Therefore, binary number 1101 has a value of 13 in the decimal system.

Similar to Eq. A.2, but with the base of 2, binary number 1101.01 can be expressed as

$\textsf{\textbf{\small{Eq. B.2:}}}$
$\textsf{ \textcolor{red}{1101.01} = (\textcolor{red}{1}\times\textcolor{blue}{2}^3) + (\textcolor{red}{1}\times\textcolor{blue}{2}^2) + (\textcolor{red}{0}\times\textcolor{blue}{2}^1) + (\textcolor{red}{1}\times\textcolor{blue}{2}^0) + (\textcolor{red}{0}\times\textcolor{blue}{2}^{-1}) + (\textcolor{red}{1}\times\textcolor{blue}{2}^{-2}) }$

which in the decimal system means

$\textsf{ \textcolor{red}{1101.01} = (\textcolor{red}{1}\times8) + (\textcolor{red}{1}\times4) + (\textcolor{red}{0}\times2) + (\textcolor{red}{1}\times1) + \left(\textcolor{red}{0}\times\frac{1}{2}\right) + \left(\textcolor{red}{1}\times\frac{1}{4}\right) }$

$\textsf{ \textcolor{red}{1101.01} = (\textcolor{red}{1}\times8) + (\textcolor{red}{1}\times4) + (\textcolor{red}{0}\times2) + (\textcolor{red}{1}\times1) + (\textcolor{red}{0}\times0.5) + (\textcolor{red}{1}\times0.25) }$

$\textsf{ (\textcolor{red}{1101.01})_{\textcolor{blue}{2}} = 8 + 4 + 1 + 0.25 = (13.25)_{\textcolor{blue}{10}} }$

Therefore, binary number 1101.01 has a decimal value of 13.25.

C. Hexadecimal Number System (Base-16 Number System)

For hexadecimal system, as the base is 16, there are 16 symbols (or digits) to be used to represent the numbers in this system, they are 0 to 9 and then A, B, C, D, E, F (not case-sensitive). Symbols A, B, C, D, E, F are used to replace 10, 11, 12, 13, 14, 15, respectively, because only single digit/symbol can be used. For instance, A1E and A1E.2D are two examples of hexadecimal numbers. Equivalent of A1E in the decimal system is:

$\textsf{ \textcolor{red}{A1E} = (\textcolor{red}{A}\times\textcolor{blue}{16}^2) + (\textcolor{red}{1}\times\textcolor{blue}{16}^1) + (\textcolor{red}{E}\times\textcolor{blue}{16}^0) }$

substitute A with 10 and E with 14, we have

$\textsf{ \textcolor{red}{A1E} = (\textcolor{red}{10}\times256) + (\textcolor{red}{1}\times16) + (\textcolor{red}{14}\times1) }$

$\textsf{ (\textcolor{red}{A1E})_{\textcolor{blue}{16}} = 2560 + 16 + 14 = (2590)_{\textcolor{blue}{10}} }$

and the equivalent of A1E.2D in the decimal system is:

$\textsf{ \textcolor{red}{A1E.2D} = (\textcolor{red}{A}\times\textcolor{blue}{16}^2) + (\textcolor{red}{1}\times\textcolor{blue}{16}^1) + (\textcolor{red}{E}\times\textcolor{blue}{16}^0) + (\textcolor{red}{2}\times\textcolor{blue}{16}^{-1}) + (\textcolor{red}{D}\times\textcolor{blue}{16}^{-2}) }$

$\textsf{ \textcolor{red}{A1E.2D} = (\textcolor{red}{10}\times256) + (\textcolor{red}{1}\times16) + (\textcolor{red}{14}\times1) + \left(\textcolor{red}{2}\times\frac{1}{16}\right) + \left(\textcolor{red}{13}\times\frac{1}{16^2}\right) }$

$\textsf{ (\textcolor{red}{A1E.2D})_{\textcolor{blue}{16}} = 2560 + 16 + 14 + 0.125 + 0.050781= (2590.175781)_{\textcolor{blue}{10}} }$

Therefore, equivalent numbers of A1E and A1E.2D in the decimal system are 2590 and 2590.175781, respectively.

D. Octal Number System (Base-8 Number System)

The Octal system has the base of 8. There are 8 digits, 0, 1, 2, 3, 4, 5, 6, 7, to be used to represent the numbers in this system. Conversion of an octal number to decimal number is carried out in the same way as for binary or hexadecimal numbers. For instance, two octal numbers 725 and 725.36 can be converted to decimal numbers as follows:

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} & 725.36 &= &(\textcolor{red}{7}\times8^2) + (\textcolor{red}{2} \times8^1) + (\textcolor{red}{5}\times8^0) + (\textcolor{red}{3}\times8^{-1}) + (\textcolor{red}{6}\times8^{-2}) \\ & &= &(\textcolor{red}{7}\times64) + (\textcolor{red}{2} \times8) + (\textcolor{red}{5}\times1) + (\textcolor{red}{3}\times0.125) + (\textcolor{red}{6}\times0.015625) \\ & &= & 448 + 16 + 5 + 0.375 + 0.09375 \\ & &= & 469.46875 \end{tabular} }$

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} \implies & (725.36)_{\textcolor{blue}{8}} &= &(469.46875)_{\textcolor{blue}{10}} \end{tabular} }$

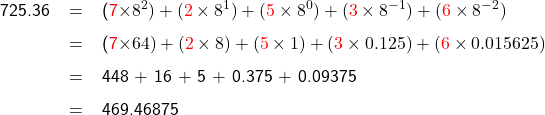
E. Other Number Systems

Theoretically, any number can be used as a base for a numbering system, and conversion of any number of any base to its equivalent decimal number follows the same method as described by Eqs A.1, A.2 or B.1, B.2 above. For example, using the described approach, quaternary numbers (base 4 numbers) 2103 and 2103.12 are found having decimal values of 147 and 147.375, respectively.

Example 1

Question: In which system is the number ‘101’ equivalent to a decimal 50?
Answer: Let x be the unknown base, where x > 0. Similar to Eq. A.1, we can write:

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} & \textcolor{red}{1}\textsf{x}^2 + \textcolor{red}{0} \textsf{x}^1 + \textcolor{red}{1} \textsf{x}^0 &= &50 \\ \therefore & x^2 + 1 &= &50 \\ \therefore & x^2 &= &49 \\ \therefore & x &= &7 \\ \end{tabular} }$

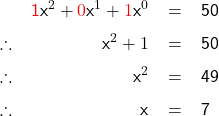
The base is 7, thus, the system is septenary system.

Example 2

Question: In which system is the number ’4704’ equivalent to a decimal 2500?
Answer: Let x be the unknown base, where x > 0. Similar to Example 1, we can write:

$\renewcommand{\arraystretch}{1.5} \textrm{ \begin{tabular}{l r c l} & \textcolor{red}{4}\textsl{x}^3 + \textcolor{red}{7} \textsl{x}^2 + \textcolor{red}{0} \textsl{x}^1 + \textcolor{red}{4} \textsl{x}^0 &= &2500 \\ \end{tabular} }$

This is a cubic equation. Analytically solving polynomial equations of degree higher than 2 can be challenging. However, for number systems, there is often a simpler approach. Note the following observations:

All bases are natural numbers greater than or equal to 2.
The greater the base, the fewer digits are typically needed to represent the same value.
If two numbers have the same number of digits, the smaller the number, the higher the base.
Each digit in a number must be less than the base.

These observations significantly reduce the time and effort needed to find the unknown base. A brute-force approach may be sufficient.

In the case of the number 4704, based on the above observations, we can infer that the unknown base x is greater than 7 and less than 10 (i.e., 7 < x < 10). Therefore, x is either 8 or 9. By substituting 8 and 9 into the equation above, we find that the correct base is 8. Thus, the system is octal.

Example 3

Question: In which system is the number ‘61d8’ equivalent to the hexadecimal 41d2?
Answer: We start with a similar approach. Let x be the unknown base, where x > 0, and replace ‘d’ with 13. Then we can write:

$\renewcommand{\arraystretch}{1.5} \textrm{ \begin{tabular}{l r c l} & \textcolor{red}{6}\textsl{x}^3 + \textcolor{red}{1} \textsl{x}^2 + \textcolor{red}{13} \textsl{x}^1 + \textcolor{red}{8} \textsl{x}^0 &= &41d2_{16} \\ \end{tabular} }$

As in Example 2, the unknown base x must be greater than 13 and less than 16 (i.e., 13 < x < 16). Therefore, x must be either 14 or 15. By testing both values, we find that the correct base is 14.

Notes:

For fractional numbers, the fractional part could be infinite. Therefore, if you want to limit the number of digits after the decimal point, a cut-off may be required. In such cases, the number and its equivalent decimal value might not be exactly equal.
The conversion of a decimal number to another number system is discussed in “Decimal Number Conversion to Other Number Systems“.
In general, a number can be converted to any other number system by using the decimal system as an intermediate step. A Python code for converting a number of any base to another number system is available h ere. In this code, the base is limited to between 2 and 16, but users can expand it for any base greater than 16, provided a system of symbols is defined for such a base accordingly.