Quadratic Equations

Deriving The solutions To a quadratic equation

Quadratic equations are equations of the form

$\texrm{(1)}\hspace{50px}\displaystyle{ax^2 + bx + c = 0}, \qquad \qquad where \qquad $a \neq 0$.$

As $a \neq 0$ , we can divide both the left hand side (LHS) and the right hand side (RHS) of the equation by $a$ , which then gives

$\texrm{(2)}\hspace{50px}\displaystyle{x^2 + \frac{b}{a}x + \frac{c}{a} = 0}$

Modifying the LHS by multiplying the second term by $\frac{2}{2}$ , and then adding and subtracting $\frac{b^2}{(2a)^{2}}$ to/from the LHS, we get

$\texrm{(3)}\hspace{50px}\displaystyle{x^2 + 2\frac{b}{2a}x + \frac{b^2}{(2a)^2} - \frac{b^2}{(2a)^2} + \frac{c}{a} = 0}$

Note that Eq. (3) is the same as Eq. (2).

Utilizing the algebraic identity $(u+v)^2 = u^2 + 2uv + v^2$ for the first three terms and making $(2a)^2$ a common denominator for the last two terms of the LHS, Eq. (3) becomes:

$\texrm{(4a)}\hspace{43px}\displaystyle{\left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2 - 4ac}{(2a)^2}\right) = 0}$

$\texrm{(4b)}\hspace{43px}\displaystyle{\left(x+\frac{b}{2a}\right)^2 - \left(\frac{\sqrt{b^2 - 4ac}}{2a}\right)^2 = 0}$

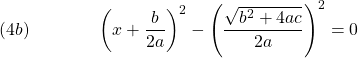
Utilizing the algebraic identity $u^2 - v^2 = (u - v)(u + v)$ Eq. (4b) becomes:

$\texrm{(5)}\hspace{50px}\displaystyle{\left(\left(x+\frac{b}{2a}\right) - \frac{\sqrt{b^2 - 4ac}}{2a}\right)\left(\left(x+\frac{b}{2a}\right) + \frac{\sqrt{b^2 - 4ac}}{2a}\right) = 0}$

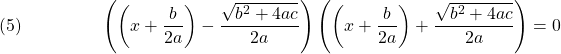
For Eq. (5) to be valid, either $\left(x+\frac{b}{2a} - \frac{\sqrt{b^2 - 4ac}}{2a}\right)$ or $\left(x+\frac{b}{2a} + \frac{\sqrt{b^2 - 4ac}}{2a}\right)$ must be equal to $0$ , therefore, the solutions to the quadratic equation are: