Derivation of the Doppler effect formulas
Contents
The Doppler effect
Derivation of the Doppler effect formulas
1. Both source and observer are at rest
2. Source approaching a stationary observer
3. Source moving away from a stationary observer
4. Observer approaching a stationary source
5. Observer moving away from a stationary source
6. Both source and observer moving towards each other
7. Both source and observer moving away from each other
8. Source approaching, observer receding
9. Source receding, observer approaching
10. Summary
Related topic
Tips For Using The Doppler Effect General Formula
The Doppler effect
The Doppler effect is the change in frequency when there is relative motion between a source of waves and an observer.
In the case of sound waves, observed frequency ![]() (i.e., the frequency that is heard by an observer from a distance), is given by
(i.e., the frequency that is heard by an observer from a distance), is given by
![]()
where ![]() is the frequency emitted by the source,
is the frequency emitted by the source, ![]() is the speed of sound (
is the speed of sound (![]() in air at 20° C),
in air at 20° C), ![]() is the speed of the observer, and
is the speed of the observer, and ![]() is the speed of the source. Equation (1) was derived on conditions that the source frequency is constant, and both source’s speed and observer’s speed must also be constant. In addition, the motion of source and observer has to be along the line joining them
is the speed of the source. Equation (1) was derived on conditions that the source frequency is constant, and both source’s speed and observer’s speed must also be constant. In addition, the motion of source and observer has to be along the line joining them
Derivation of the Doppler effect formulas
Derivation of Eq. (1) in the following section is for sound waves and when the motion of source and observer is along the line joining the two.
Case 1: Both source and observer are at rest
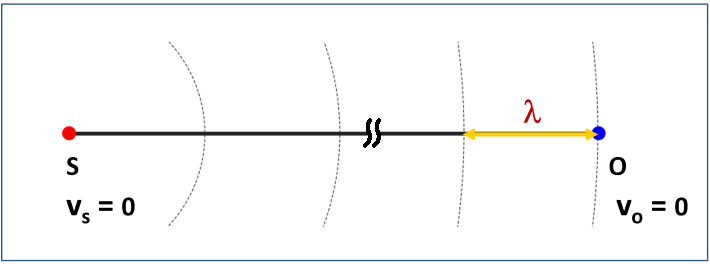
The speed of a sound wave ![]() can be expressed as
can be expressed as
![]()
where ![]() is the wave wavelength, that is the distance between the two consecutive wave fronts (the yellow double arrow in Fig. 1) and
is the wave wavelength, that is the distance between the two consecutive wave fronts (the yellow double arrow in Fig. 1) and ![]() is the wave frequency. Rearranging Eq (2),
is the wave frequency. Rearranging Eq (2), ![]() can be expressed as
can be expressed as
![]()
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() be the wavelength and frequency of the sound wave emitted by the source and the wavelength and frequency heard by an observer from a distance from the source, respectively. If both source and observer are at rest, then
be the wavelength and frequency of the sound wave emitted by the source and the wavelength and frequency heard by an observer from a distance from the source, respectively. If both source and observer are at rest, then
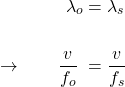
or
![]()
The observer in this case will hear a sound of the same pitch (same frequency) as that of the source. ![]() is the source wavelength, depicted by the yellow double arrow in all Figures in this Section.
is the source wavelength, depicted by the yellow double arrow in all Figures in this Section.
Case 2: Source approaching a stationary observer
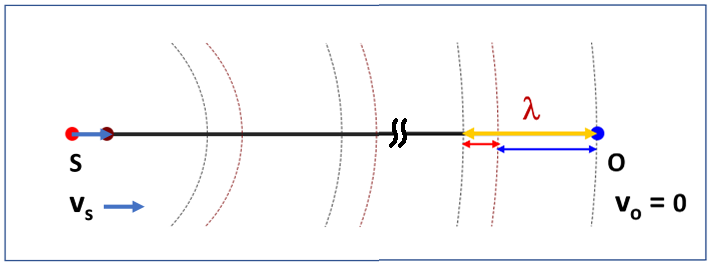
As shown in Fig. 2, when the source is approaching an observer at a constant speed ![]() , the sound wave fronts (dark red dotted lines) will travel a distance
, the sound wave fronts (dark red dotted lines) will travel a distance ![]() (red double arrow) ahead of the wave fronts already emitted (grey dotted lines). Note that, sound wave motion after leaving the source is governed by the medium (e.g., air) properties, and is not affected by the source’s motion. Since in one wave period, sound waves travel one
(red double arrow) ahead of the wave fronts already emitted (grey dotted lines). Note that, sound wave motion after leaving the source is governed by the medium (e.g., air) properties, and is not affected by the source’s motion. Since in one wave period, sound waves travel one ![]() , distance
, distance ![]() can be related to source wavelength as
can be related to source wavelength as ![]() . Therefore
. Therefore
![]()
or
![]()
On the observer end, the distance between the consecutive wave fronts, i.e., the new wavelength ![]() (depicted by the blue double arrow) now becomes
(depicted by the blue double arrow) now becomes ![]() . As
. As ![]() , we have
, we have
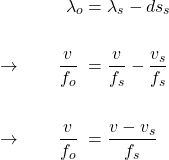
or
![]()
As ![]() ,
, ![]() is greater than
is greater than ![]() , which means observer hears sounds of a higher pitch than it actually is.
, which means observer hears sounds of a higher pitch than it actually is.
Case 3: Source moving away from a stationary observer
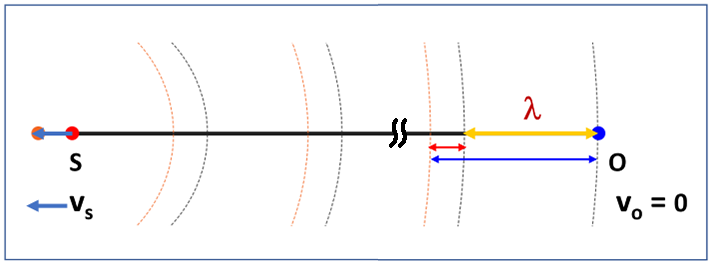
As seen in Fig. 3, when source moves away from observer at a constant speed ![]() , the new sound wave fronts (orange dotted lines) also move further away from observer a distance
, the new sound wave fronts (orange dotted lines) also move further away from observer a distance ![]() . As a result, the new observed wavelength
. As a result, the new observed wavelength ![]() becomes
becomes ![]() , combined that with Eq. (5), we have
, combined that with Eq. (5), we have
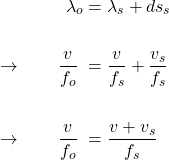
or
![]()
In Eq. 7, ![]() , therefore,
, therefore, ![]() , the observer hears sounds at a lower pitch than it is at the source.
, the observer hears sounds at a lower pitch than it is at the source.
Case 4: Observer approaching a stationary source
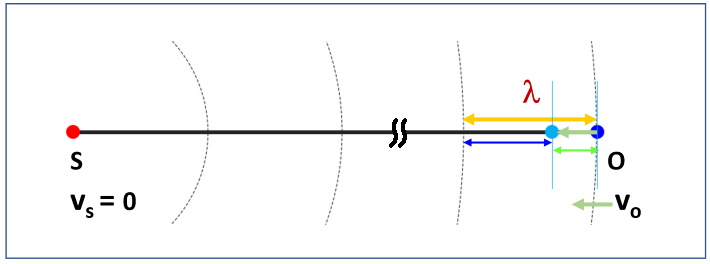
In this case, source is stationary, observer moves towards it at a constant speed ![]() . For one wave period, observer travels a distance
. For one wave period, observer travels a distance ![]() (bright green double arrow). As wavelength
(bright green double arrow). As wavelength ![]() is the distance the observed wave travels for one wave period,
is the distance the observed wave travels for one wave period, ![]() can be related to
can be related to ![]() as
as ![]() , therefore
, therefore
![]()
or
![]()
Now, on observer end, ![]() becomes
becomes ![]() , we have
, we have
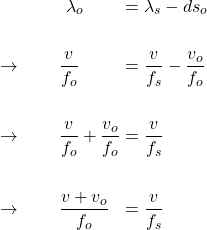
or
![]()
Since ![]() ,
, ![]() , observer hears sounds of a higher pitch than it is at the source.
, observer hears sounds of a higher pitch than it is at the source.
Case 5: Observer moving away from a stationary source
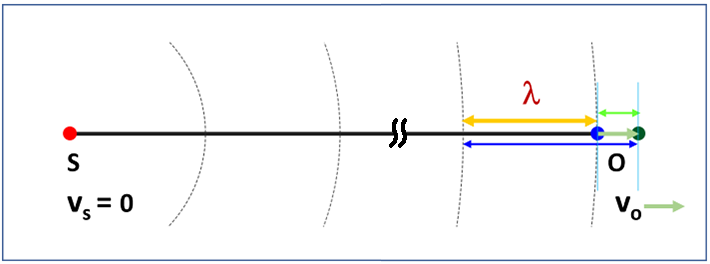
In this case, source is stationary and observer is approaching source at a constant speed ![]() . As shown in Fig. 5, observer’s new wavelength
. As shown in Fig. 5, observer’s new wavelength ![]() now becomes (
now becomes (![]() ), combined that with Eq. (8) we have
), combined that with Eq. (8) we have
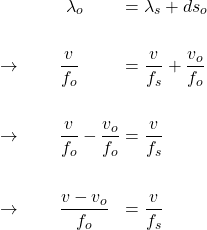
or
![]()
Since ![]() ,
, ![]() , observer hears a lower pitch sound.
, observer hears a lower pitch sound.
Case 6: Both source and observer moving towards each other
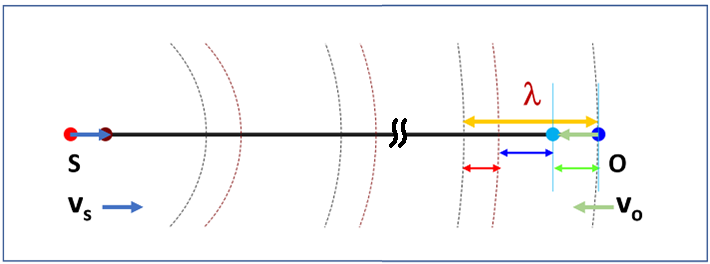
In this case, source is approaching observer at constant speed ![]() and observer is moving towards the source at a constant speed
and observer is moving towards the source at a constant speed ![]() . As seen in Fig. 6, observer’s new wavelength
. As seen in Fig. 6, observer’s new wavelength ![]() is equal to (
is equal to (![]() ), and we have
), and we have
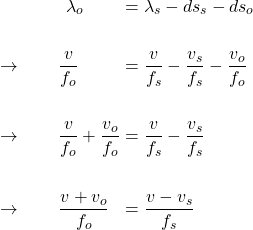
or
![]()
Since ![]() ,
, ![]() , observer hears sounds of a higher pitch.
, observer hears sounds of a higher pitch.
Case 7: Both source and observer moving away from each other
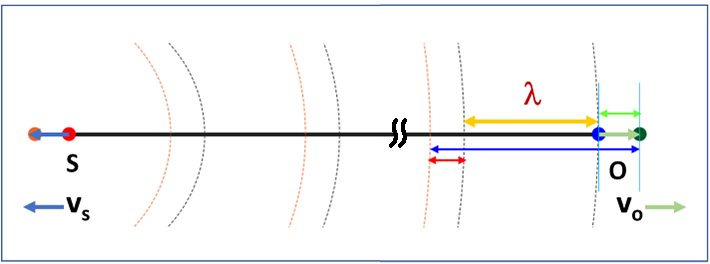
In this case, source is receding from observer at a constant speed ![]() and observer is also moving away from source at a constant speed
and observer is also moving away from source at a constant speed ![]() . As seen in Fig. 7, observer’s new wavelength
. As seen in Fig. 7, observer’s new wavelength ![]() is now equal to (
is now equal to (![]() ), so we have
), so we have
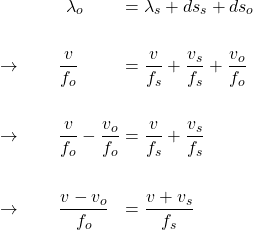
or
![]()
Since ![]() ,
, ![]() , observer hears a lower pitch sound.
, observer hears a lower pitch sound.
Case 8: Source approaching, observer receding
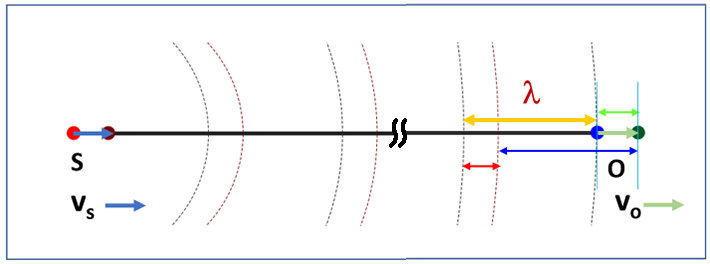
In this case, source is approaching observer at a constant speed ![]() but observer is moving away from source at a constant speed
but observer is moving away from source at a constant speed ![]() . As seen in Fig. 8, observer’s new wavelength
. As seen in Fig. 8, observer’s new wavelength ![]() is now equal to (
is now equal to (![]() ), so we have
), so we have
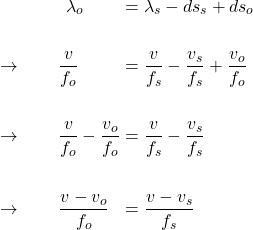
or
![]()
In this case, if ![]() , then the net effect is approaching, therefore,
, then the net effect is approaching, therefore, ![]() , observer hears a higher pitch sound. The opposite occurs if
, observer hears a higher pitch sound. The opposite occurs if ![]()
Case 9: Source receding, observer approaching
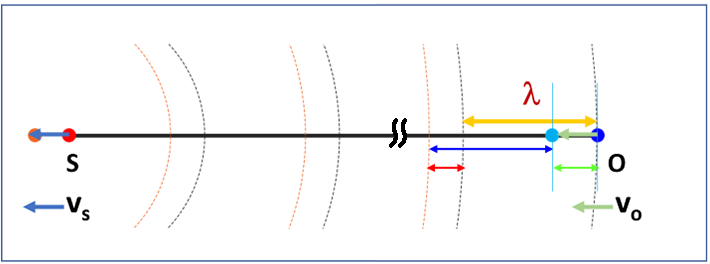
In this case, source is receding from observer at constant speed ![]() while observer is moving towards source at a constant speed
while observer is moving towards source at a constant speed ![]() . As shown in Fig. 9, observer’s new wavelength
. As shown in Fig. 9, observer’s new wavelength ![]() is now equal to (
is now equal to (![]() ), and we have
), and we have
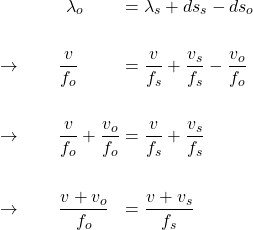
or
![]()
In this case, if ![]() , then the net effect is receding, therefore,
, then the net effect is receding, therefore, ![]() , observer hears a higher pitch sound. The opposite occurs if
, observer hears a higher pitch sound. The opposite occurs if ![]()
Summary
Combining Eqs. (6), (7), and (9) – (14) we have
![]()
This is the same general equation (Eq. 1) mentioned earlier in the introduction part of the Doppler effect, which combines all relative motions between a sound wave source and an observer along the straight line joining the two.
You can find tips on quickly extracting the Doppler effect equation for a specific relative motion between the sound source and an observer from this general equation here.
