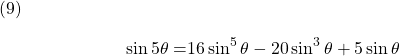The De Moivre’s Theorem
Question
Express cos (5θ) and sin (5θ) in terms of cos (θ) and sin (θ).
Answer
Using the De Moivre’s Theorem:
![]()
where ![]() is an imaginary number and has a value of
is an imaginary number and has a value of ![]() , or
, or ![]() −1, we can write
−1, we can write
![]()
Expanding the right hand side (RHS) of the equation (2) gives
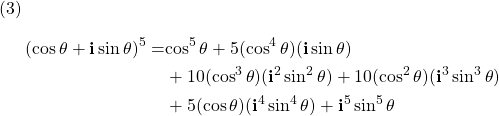
Noting that ![]() −1, therefore,
−1, therefore, ![]() −
− ![]() ,
, ![]() , and
, and ![]() , Eq. (3) can be written as
, Eq. (3) can be written as
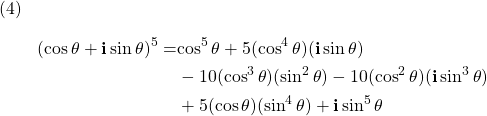
Substitute the left hand side (LHS) of Eq. 4 with ![]() (De Moivre’s Theorem) and grouping the real part (
(De Moivre’s Theorem) and grouping the real part (![]() ) and imaginary part (
) and imaginary part (![]() ) on the right hand side (RHS), we have
) on the right hand side (RHS), we have
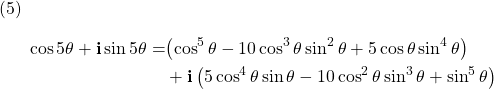
For Eq. (5) to be valid the ![]() and
and ![]() parts on the LHS and RHS of the equation must be respectively equal, that is
parts on the LHS and RHS of the equation must be respectively equal, that is
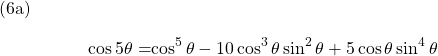
and
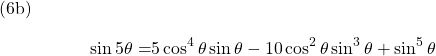
Making use of the trigonometric identities ![]() –
– ![]() , and
, and ![]() –
– ![]() –
– ![]() , Eq. (6a) becomes
, Eq. (6a) becomes
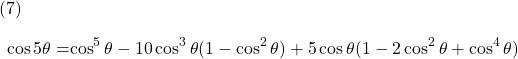
which can be further simplified to give the expression for ![]() in terms of
in terms of ![]() as:
as:
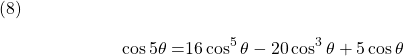
Similarly, making use of the trigonometric identity ![]() –
– ![]() , expression for
, expression for ![]() in terms of
in terms of ![]() is
is