Calculating force of impact

PROBLEM

A 500 g cart is released from rest 1.0 m from the bottom of a frictionless, 30.0 degree ramp. The cart rolls down the ramp and bounces off a rubber block at the bottom. After the cart bounces, it rolls back up the ramp and stops at 0.5 m from the bottom of the ramp (before rolling down again). Calculate the average force of impact on the rubber block, given the collision duration is 26.7 ms.

VISUALIZE

Figures 1a and 1b depict the cart at the start position, before rolling down the ramp, and after bouncing off the rubber block, respectively.

**Figure 1a:**
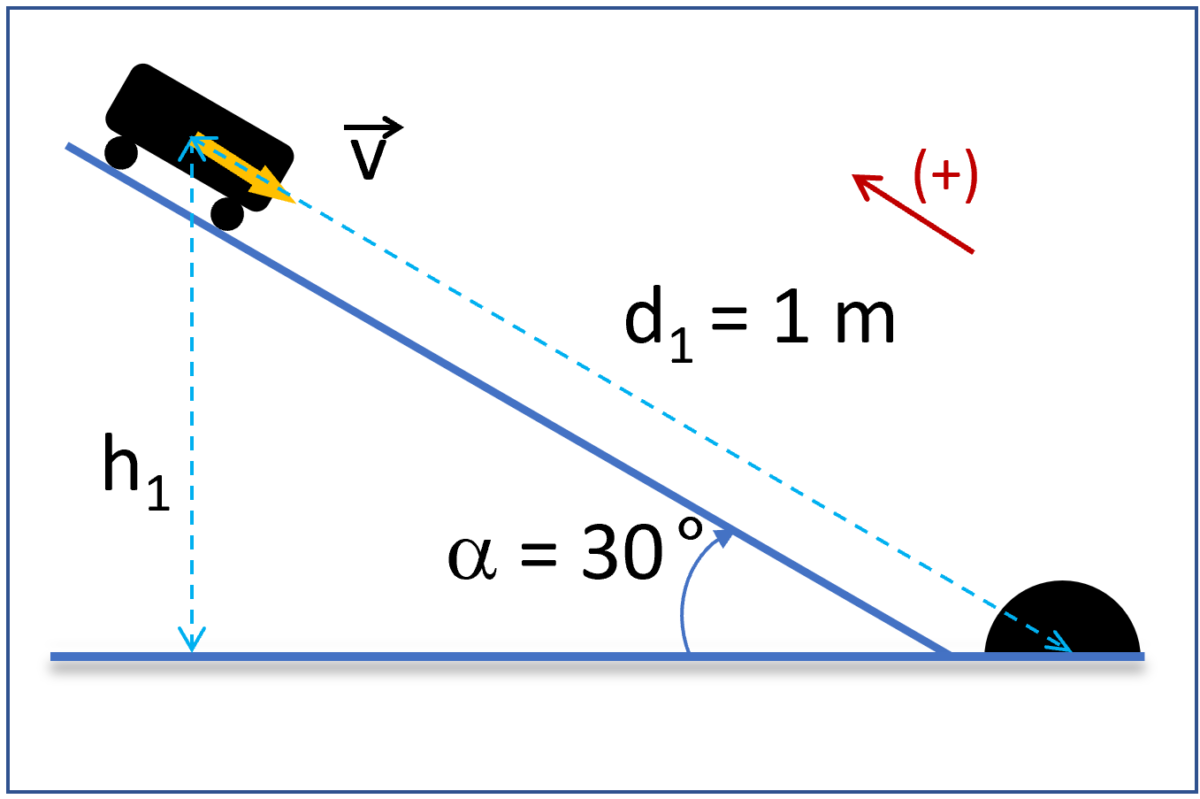
The cart at start position before rolling down the ramp due to gravity

**Figure 1b:**
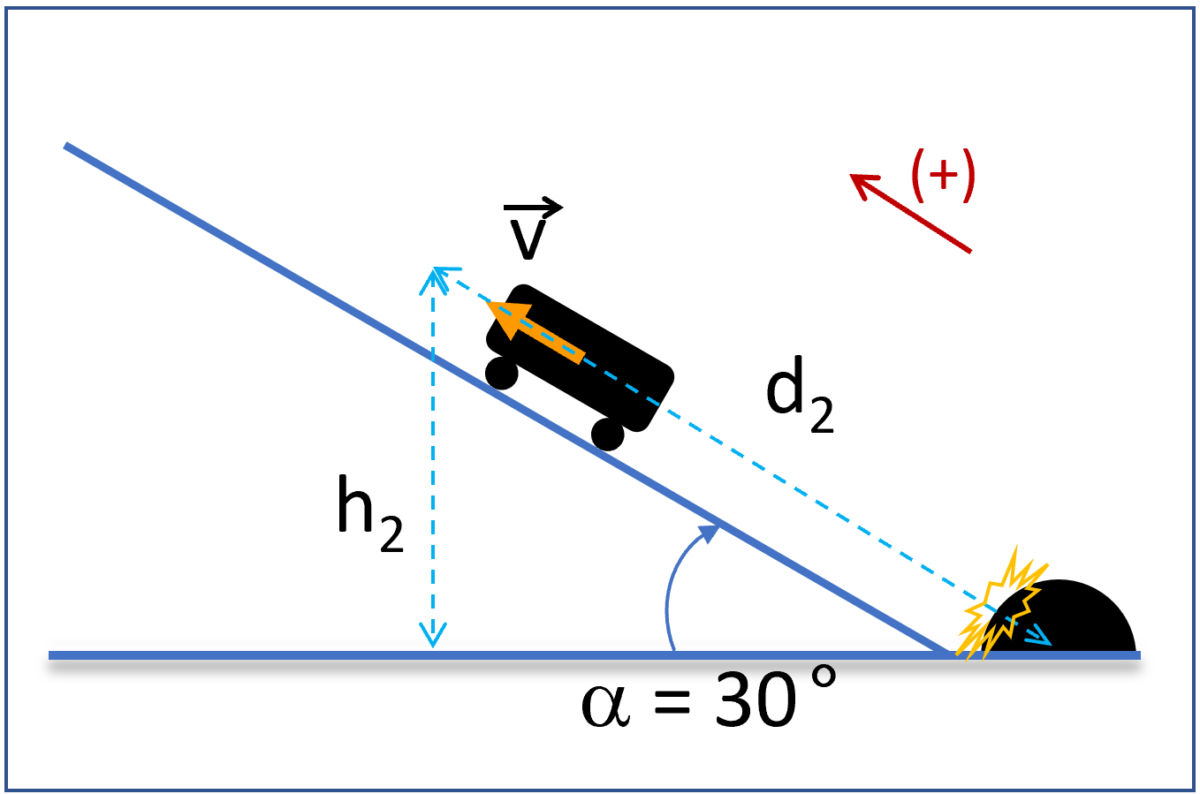
The cart rolling back up the ramp after colliding with the rubber block

SOLVE

Since thermal energy is not considered (frictionless ramp), the cart’s system energy is the same as its mechanical energy, which is a sum of its gravitational energy and kinetic energy. As a result, the cart can be modeled as a particle with its total mass being at its center of mass, and its collision with the rubber block takes place at the ground level ( $h = 0$ ). Let’s choose positive direction as shown by the red arrow in Figures 1a and 1b (up the ramp).

$\textbf{Given:}$

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} Mass: &$m$& = & $500$ g $ = 0.5$ kg \\ Collision duration: &$\Delta t$ & = & $26.7$ ms $ = 26.7\times10^{-3}$ s \\ Distance: &$d_{1}$ & = & $1.0$ m \\ Distance: &$d_{2}$ & = & $0.5$ m \end{tabular} }$

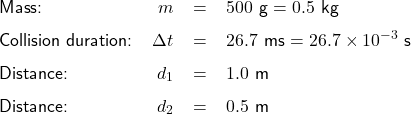
The cart’s Mechanical Energy $=$ Gravitational Energy + Kinetic Energy

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} &$ E $& = & $U + K$ \\ & $$ & = & $mgh + \frac{1}{2}mv^{2}$ \end{tabular} }$

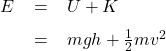
At the begining, the cart is at rest, $v = 0$ , hence $K = 0$ , therefore the cart’s mechanical energy is

$\renewcommand{\arraystretch}{1.5}\textsf{ $E = U = mgh_{1} = mgd_{1}\sin\alpha$ }$

When the cart reaches the bottom of the ramp, $h = 0$ , hence $U = 0$ , all gravitational energy is transformed into kinetic energy. Let $\vec{v}_{1}$ be the velocity of the cart immediately before the collision with the rubber block, and $v_{1} = |\vec{v}_{1}|$ (magnitude of velocity) then

$\renewcommand{\arraystretch}{1.5}\textsf{ \begin{tabular}{l r c l} \quad & $K_{1}$& = &$E$ \\ & $\frac{1}{2}mv_{1}^{2}$ & = &$mgh_{1}$ \\ & & = &$mgd_{1}\sin\alpha$ \\ or & $v_{1} $ & = & $\sqrt{2gd_{1}\sin\alpha}$ \\ & & = & $\sqrt{2\times9.8\times1.0\times0.5}$ \\ & & = & $3.13$ m/s, in negative direction \end{tabular} }$

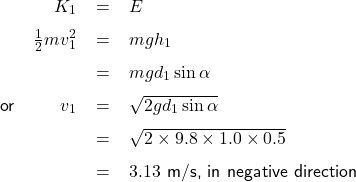
After the collision, the cart rolls back up the ramp and stops at distance $d_{2}$ from the bottom of the ramp, at that point all kinetic energy of the cart remaining after the collision ( $K_{2}$ ) transforms back to the gravitational energy ( $U_{2}$ ).
Let $\vec{v}_{2}$ be the velocity of the cart right after the collision, and $v_{2} = |\vec{v}_{2}|$ , then

$\renewcommand{\arraystretch}{1.5}\textsf{ \begin{tabular}{l r c l} \quad & $K_{2}$& = &$U_{2}$ \\ & $\frac{1}{2}mv_{2}^{2}$ & = &$mgh_{2}$ \\ & & = &$mgd_{2}\sin\alpha$ \\ or & $v_{2} $ & = & $\sqrt{2gd_{2}\sin\alpha}$ \\ & & = & $\sqrt{2\times9.8\times0.5\times0.5}$ \\ & & = & $2.21$ m/s, in positive direction \end{tabular} }$

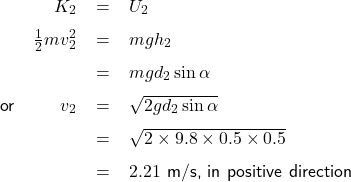
After the collision, the momentum of the cart changes (velocity changes both in magnitude and in direction).

$\textsf{ \begin{tabular}{l r c l} &$\Delta\vec{p}$ & = & $m(\vec{v}_{2} - \vec{v}_{1})$ \\ \therefore &$\Delta p$ & = & $m(v_{2} - v_{1})$ \\ & & = & $0.5(2.21 - (-3.13))$ \\ & & = & $2.67$ kgm/s \end{tabular} }$

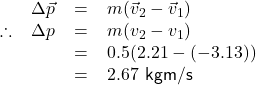
As change in momentum in the cart is equal to the impulse $I_{cart}$ upon the cart. A positive value of $I_{cart}$ means during the collision duration the cart experiences an impact force $\vec{F}_{cart}$ in the positive direction (up the ramp).

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} & $I_{cart}$ & = & $\Delta p$ \\ or & $\overline{F}_{cart}\Delta t$ & = & $2.67$ Ns \\ \therefore &$\overline{F}_{cart}$ & = & $\frac{2.67}{26.7\times10^{-3}}$ N \\ & & = & $100.0$ N \end{tabular} }$

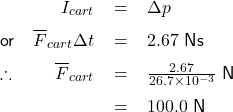
Note that the magnitude of the force of impact $\vec{F}_{cart}$ may vary during the collision, so an average force $\overline{F}_{cart}$ is used here.
According to Newton’s $\emph{third law of motion}$ , during the collision the rubber block also experiences a force of impact $\vec{F}_{rb}$ , which is equal to but in the opposite direction of $\vec{F}_{cart}$ .

Thus,

$\renewcommand{\arraystretch}{1.5} \textsf{ \begin{tabular}{l r c l} & $\overline{F}_{rb}$ & = & $-\overline{F}_{cart}$ \\ or & $\overline{F}_{rb}$ & = & $-100.0$ N \end{tabular} }$

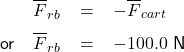
Conclusion: the average force of impact on the rubber block is 100.0 N toward the ground (negative direction).