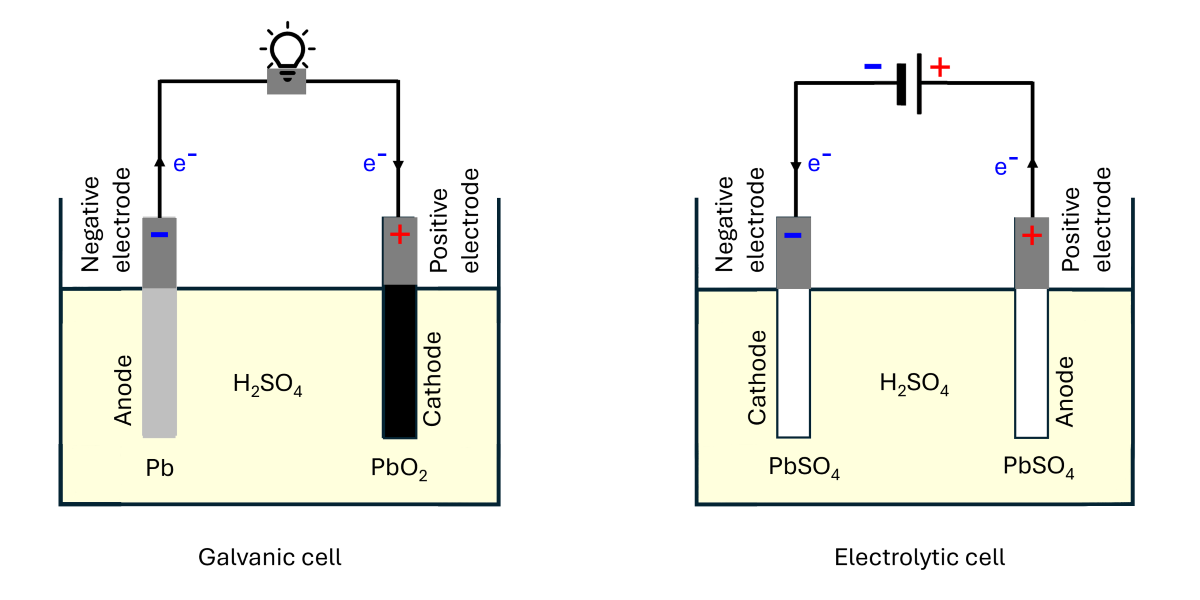
Redox reactions in a lead – acid cell
Problem
A lead-acid battery consists of 6 secondary (rechargeable) cells connected together in a series. The overall discharge (spontaneous) reaction equation for a lead-acid cell is
![]()
- Identify the oxidant and reductant in the above redox reaction; identify the anode and the cathode, and the negative and positive electrodes of the cell.
- Write the half-reactions at the anode and the cathode sites of the cell.
- Using data from the electrochemical series, calculate the voltage at standard conditions produced by a single lead-acid cell, and by the battery.
- What is the discharge voltage of this battery if the acid concentration is 3 molal (≈ 2.7 M), at 25°C?
Solution
Sulfuric Acid as a Diprotic
Solution provided in the following Section is based on the rigorous model, which treats sulfuric acid as a diprotic acid. Redox reactions in a lead-acid cell can also be described slightly differently using the approximate model, which treats sulfuric acid as a strong monoprotic acid. Solution based on the latter model can be found here.
1. Oxidant & reductant in the redox reaction in a lead-acid cell, the cell’s anode & cathode, and negative & positive electrodes
To identify an oxidant (oxidizing agent) or a reductant (reducing agent) in a redox reaction, we calculate the oxidation number of each atom in each reactant and see how they change after the reaction. A change in oxidation number of an atom after the reaction will tell whether it is an oxidant (if its oxidation number decreases), or a reductant (if its oxidation number increases). On how to calculate oxidation numbers of an atom in an ion, monatomic or polyatomic, or in a compound, see these examples. An oxidation number of an atom is also known as the oxidation state of that atom.
With regard to the redox reaction equation (Eq.1) in the lead-acid cell:
![]()
the reactants are Pb(s), PbO![]() (s), SO
(s), SO![]() (aq), and H
(aq), and H![]() (aq), and the products are PbSO
(aq), and the products are PbSO![]() (s) and H
(s) and H![]() O(l).
O(l).
Oxidation number of Pb in metal Pb is 0, in solid PbO![]() is +4, and in solid PbSO
is +4, and in solid PbSO![]() is +2
is +2
Oxidation numbers of S (Sulfur), O (Oxygen), and H (Hydrogen) do not change in this reaction.
Oxidant & Reductant | Anode & Cathode
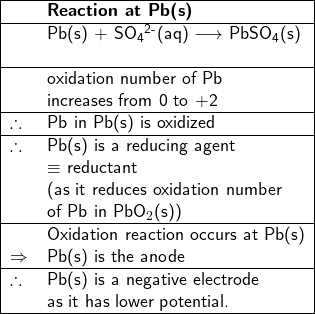
Since the oxidation number of Pb increases from zero in metal Pb(s) to +2 in PbSO![]() (s), Pb(s) is oxidized, therefore, it is a reductant (or a reducing agent). Thus, the reaction between Pb(s) and SO
(s), Pb(s) is oxidized, therefore, it is a reductant (or a reducing agent). Thus, the reaction between Pb(s) and SO![]() (aq) at the Pb metal site to form PbSO
(aq) at the Pb metal site to form PbSO![]() (s) is an oxidation reaction, therefore Pb(s) is the anode, where electrons are produced.
(s) is an oxidation reaction, therefore Pb(s) is the anode, where electrons are produced.
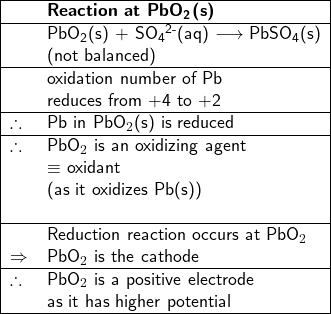
On the other hand, the oxidation number of Pb in PbO![]() (s) reduces from +4 to +2 in PbSO
(s) reduces from +4 to +2 in PbSO![]() (s), PbO
(s), PbO![]() (s) is reduced, therefore, it is an oxidant (or an oxidizing agent), thus the reaction between PbO
(s) is reduced, therefore, it is an oxidant (or an oxidizing agent), thus the reaction between PbO![]() (s) and SO
(s) and SO![]() (aq) at the PbO
(aq) at the PbO![]() (s) site to form PbSO
(s) site to form PbSO![]() (s) and water is a reduction reaction, therefore PbO
(s) and water is a reduction reaction, therefore PbO![]() (s) is a the cathode, where electrons are consumed.
(s) is a the cathode, where electrons are consumed.
Negative and positive electrodes (Electrode polarity)
In the discharge process, if the Pb site (anode) is connected to one end of an external load by a conductive wire while the PbO![]() (cathode) connected to the other end of the load, electrons will flow from the anode to the cathode through the load. Therefore, the electric current direction is from the cathode to the anode. This means that in the discharge process, the cathode has a higher potential, making it the positive electrode of the cell. On the other hand, the anode has a lower potential, making it the negative electrode.
(cathode) connected to the other end of the load, electrons will flow from the anode to the cathode through the load. Therefore, the electric current direction is from the cathode to the anode. This means that in the discharge process, the cathode has a higher potential, making it the positive electrode of the cell. On the other hand, the anode has a lower potential, making it the negative electrode.
As shown in the image below, during the recharge process, when the cell is connected to a DC source, Pb is connected to the negative terminal (lower potential), while PbO₂ is connected to the positive terminal (higher potential). The power supplied by the source causes the half-redox reactions at Pb and PbO₂ to reverse. As a result, the anode and cathode in the cell switch roles (i.e., the anode becomes the cathode and vice versa). However, the negative and positive electrodes remain unchanged. In other words, during the recharge process, the Pb site becomes the cathode but remains the negative electrode of the cell (it has the same potential as the DC negative terminal, assuming negligible potential loss along the connecting wire), and the PbO₂ site becomes the anode but remains the positive electrode (it has the same potential as the DC positive terminal).
Details of oxidation and reduction processes of the redox reaction are tabulated in Table 1.
Table 1: Summary of redox reactions at Pb(s) and PbO2(s) in a lead-acid cell.
2. Write half-reactions at the anode and cathode
Writing half reactions of a redox reaction could be challenging, so a systematic approach is usually employed to assist students step by step as follows
Write skeletal equations involving only reductant Pb(s), and oxidant PbO2; except for H and O, balance each half reaction for all elements; balance oxidation numbers by adding electrons (oxidation number is shown in red in following half reaction equations)
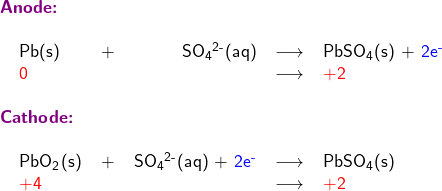
Balance each half reaction for O (oxygen) by adding water H2O (l)
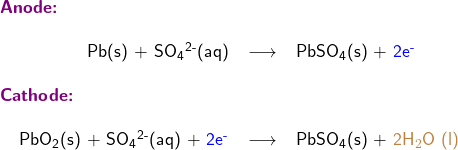
Balance each half reaction for H (hydrogen) by adding hydrogen ion H+(aq)
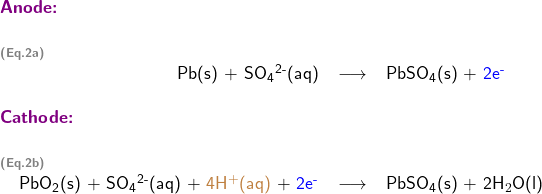
Step 4:
If the redox reaction takes place in basic medium, a further step is required to neutralize hydrogen ion H![]() by adding hydroxide ion OH
by adding hydroxide ion OH![]() to
to ![]() sides of the half reaction that has the hydrogen ion H
sides of the half reaction that has the hydrogen ion H![]() .
.
As the redox reactions in the lead-acid cell take place in an acidic medium, this step is not required.
Adding the two half reactions together to form the overall equation for the redox reaction
Multiplication of one or both half reactions may be needed to remove electrons from the overall reaction equation.

3. Calculate the standard potential of the redox reaction
The Electrochemical Series lists standard potential for reduction half-reactions. The half-reaction at the anode is an oxidation reaction Pb(s) + SO42-(aq) → PbSO4(s) + 2e–. To find its standard potential E°anode in the Electrochemical Series Table, we need to look for the standard potential of its reduction counterpart, which is the reverse reaction: PbSO4(s) + 2e– → Pb(s) + SO42-(aq). This reverse reaction has a standard potential E° of -0.3505 V.
To find the standard potential E°cathode, we note that at the cathode, the half-reaction is: PbO2(s) + SO42-(aq) + 4H+(aq) + 2e– → PbSO4(s) + 2H2O(l), which has a standard potential E° of +1.69 V, as listed in the Electrochemical Series.
The standard potential of a lead-acid cell is therefore,
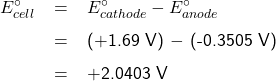
or
E![]() +2.04 V (rounded to 2 decimal places), hence, E
+2.04 V (rounded to 2 decimal places), hence, E![]() 2.04
2.04 ![]() 6
6 ![]() +12.24 V
+12.24 V
4. Calculate discharge voltage at 25 °C and 3 molal H2SO4
To calculate the cell potential (discharge voltage) at non standard conditions, we use the Nernst Equation
![]()
where

With regard to the reaction quotient, for a reversible reaction described by
![]()
a simplified expression of the reaction quotient Q is
![]()
where ![]() is the stoic reaction quotient; subscript c denotes the use of molar concentrations in the expression; and
is the stoic reaction quotient; subscript c denotes the use of molar concentrations in the expression; and ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the molar concentration of
are the molar concentration of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively
, respectively
In rigorous calculation of the reaction quotient ![]() , the activity is used in place of the concentration. Thus, the rigorous expression of
, the activity is used in place of the concentration. Thus, the rigorous expression of ![]() for Eq.1 is
for Eq.1 is
![]()
where ![]() is the activity of respective species.
is the activity of respective species.
The activity ![]() of a pure liquid or solid at its standard state is constant and equal to 1.
of a pure liquid or solid at its standard state is constant and equal to 1.
![]()
![]() is not considered as pure as there are solutes in it. Thus, the expression for
is not considered as pure as there are solutes in it. Thus, the expression for ![]() becomes
becomes
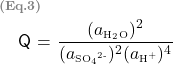
The activity ![]() of a solute
of a solute ![]() is related to its molality
is related to its molality ![]() by
by
![]()
The activity coefficient ![]() is incorporated into the solute activity formula to account for deviations from ideality.
is incorporated into the solute activity formula to account for deviations from ideality. ![]() is the standard state of 1 molal (
is the standard state of 1 molal (![]() 1 mol kg
1 mol kg![]() ), a hypothetical state in which solutes behave ideally. As a result,
), a hypothetical state in which solutes behave ideally. As a result, ![]() is dimensionless (has no unit).
is dimensionless (has no unit).
For dilute solutions (≤ 0.001M), or moderately dilute solutions (≤ 0.1M), the activity coefficient of an ion can be calculated by using the limiting Debye-Huckel equation or the extended Debye-Huckel equation, respectively. For higher concentrations, the activity coefficient can be obtained from experiments. However, the activity coefficient of an individual ion is almost impossible to measure experimentally because in solution ions are surrounded by ions of opposite sign. For that reason, the mean activity coefficient ![]() , which can be measured and available in the literature for a wide range of compounds, is used instead. For a compound
, which can be measured and available in the literature for a wide range of compounds, is used instead. For a compound ![]() , if
, if ![]() is the activity coefficient of the cation (ion with positive charge) and
is the activity coefficient of the cation (ion with positive charge) and ![]() of the anion (negative charge), then
of the anion (negative charge), then ![]() is related to
is related to ![]() and
and ![]() by
by
![]()
Thus, for ![]() , activities of ions
, activities of ions ![]() and
and ![]() are
are
![]()
and
![]()
where ![]() and
and ![]() are the activity coefficients of ions
are the activity coefficients of ions ![]() and
and ![]() , respectively,
, respectively, ![]() is the
is the ![]() molality, and
molality, and ![]() is the standard concentration of 1 molal. Using Eq.4, the mean activity coefficient of
is the standard concentration of 1 molal. Using Eq.4, the mean activity coefficient of ![]() can be derived as
can be derived as
![]()
The reaction quotient in Eq.3 becomes
![Rendered by QuickLaTeX.com \renewcommand{\arraystretch}{1.5} \textsf{Q} = $\displaystyle \frac{(a\textsubscript{\tiny{H\textsubscript{2}O}})\textsuperscript{2}}{\left[4\left(\displaystyle \frac{\gamma_{\pm} m} {m^{\circ}}\right)^{3}\right]^{2}}$](https://studycorner.com.au/wp-content/ql-cache/quicklatex.com-1edf4f16e452b6253a54ed9e937b516c_l3.png)
Using data from Treptow [Treptow, R.S., 2002], at ![]() molal,
molal, ![]() is 0.85174, and
is 0.85174, and ![]() is 0.1337, which result in Q = 10.8888
is 0.1337, which result in Q = 10.8888
Substituting values of E°cell = +2.0403 V; R = 8.314463 J.K-1mol-1; T = 25 + 273.15 = 298.15 K; n = 2; F = 96485.33 C.mol-1; and Q = 10.8888 into the Nernst equation, we get
![]()
or
E![]() +2.01 V (rounded to 2 decimal places), hence, E
+2.01 V (rounded to 2 decimal places), hence, E![]() 2.01
2.01 ![]() 6
6 ![]() +12.06 V
+12.06 V
For different concentrations, you can use the graph in Treptow’s article to estimate the water activity and the mean activity coefficient of aqueous sulfuric acid in relation to sulfuric acid concentration (refer to Figure 1). A tool to extract data from the graph can be found here.
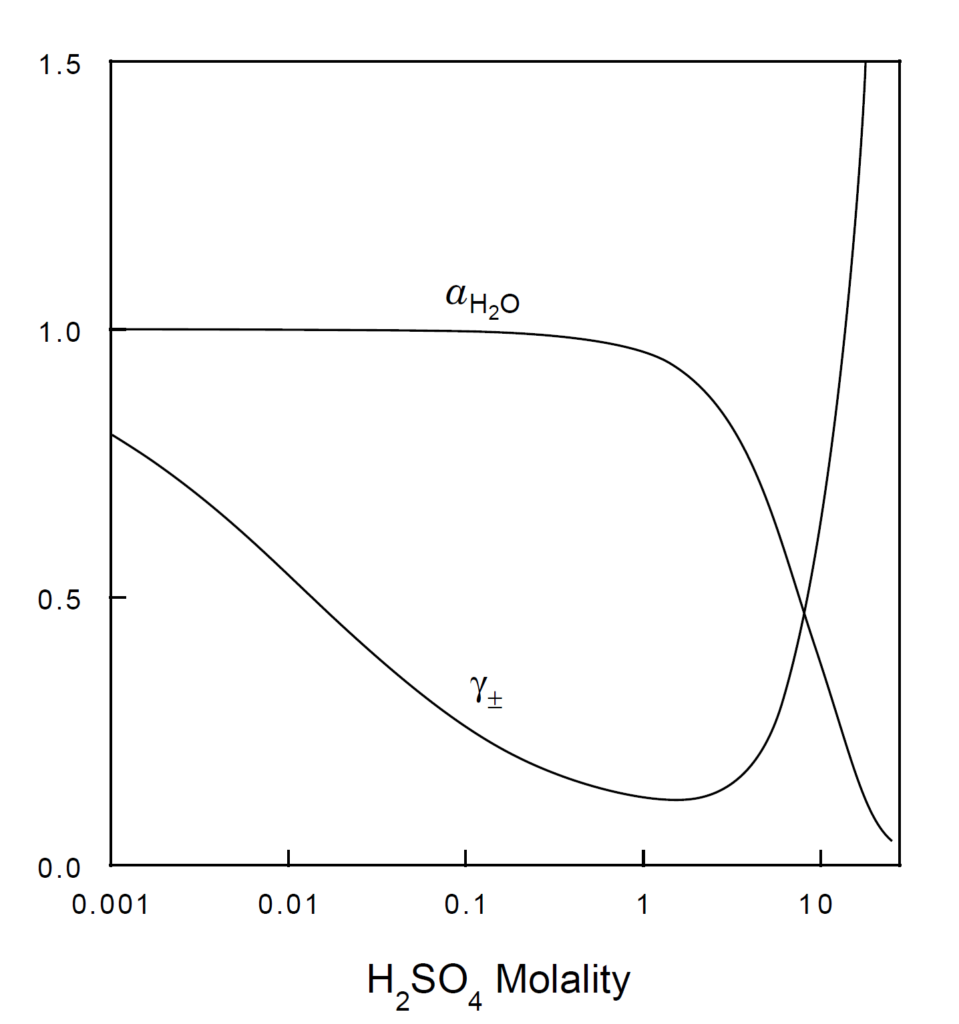
Figure 1:
Plots of the activity of water and the mean activity coefficient of sulfuric acid versus the acid molality. [Treptow, R.S., 2002]
Keep in mind that graphs are primarily used to visualize trends between variables. When extracting data from curves on these graphs, be aware that there may be small errors introduced by the common smoothing techniques used in plotting, especially for non-linear relationships
Sulfuric Acid as a Monoprotic
The reaction equation Eq.1 and the two half-reactions Eq.2a and Eq.2b are written using the rigorous model, which acknowledges that sulfuric acid is a diprotic acid and able to fully dissociate into 2H![]() and SO
and SO![]() .
.
There is another model, called the approximate model, which is also used to describe the redox reactions in the lead-acid cell. The approximate model is based on an assumption that sulfuric acid can be treated as a strong monoprotic acid, and it can completely dissociate into H![]() and HSO
and HSO![]() . Using the approximate model, the two half-reactions taking place in the lead-acid cell can be written as
. Using the approximate model, the two half-reactions taking place in the lead-acid cell can be written as
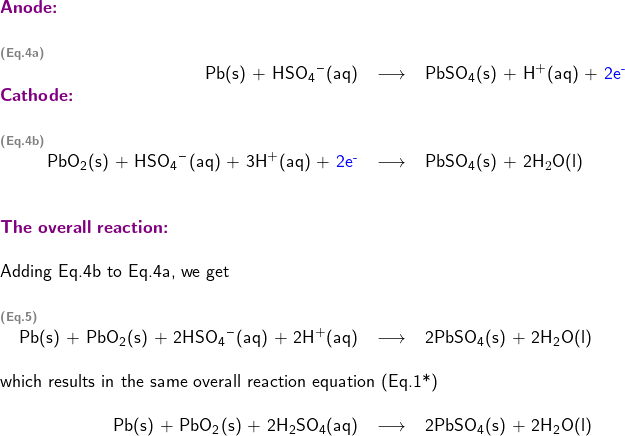
Calculate the lead-acid cell’s standard potential
The standard reduction potentials of the half reactions Eq. 4a and Eq. 4b are not listed in the electrochemical series table, so, we will calculate the cell standard potential by using the standard free-energy change for the reaction.
The cell standard potential is related to the standard free-energy change for the reaction by
![]()
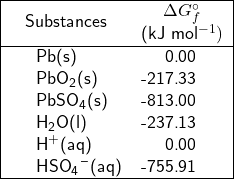
The standard free-energy change ![]() for the reaction can be calculated from the standard free-energy of formation
for the reaction can be calculated from the standard free-energy of formation ![]() of each species involved and produced in the reaction.
of each species involved and produced in the reaction.
![]()
Values of the standard free-energy of formation for these species can be found in many textbooks, handbooks, or online resources, and they are listed in Table 2 below.
Table 2: Standard Free-Energy of Formation
Using the values of standard free-energy of formation listed in Table 2, the ![]() for the reaction described by Eq.5 is calculated as follows
for the reaction described by Eq.5 is calculated as follows
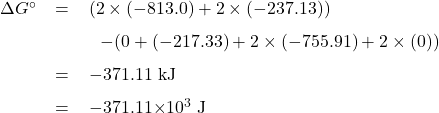
Rearranging Eq. 6, and substituting ![]() with its value of -371.11
with its value of -371.11![]() 10
10![]() J, we get
J, we get
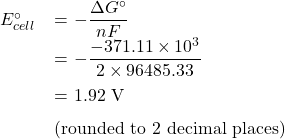
or
E![]() +1.92 V (rounded to 2 decimal places), hence, E
+1.92 V (rounded to 2 decimal places), hence, E![]() 1.92
1.92 ![]() 6
6 ![]() +11.52 V
+11.52 V
Calculate the cell discharge voltage at 25 °C and 3 molal H2SO4
The reaction quotient for Eq. 5 is
![]()
The activity ![]() of a pure liquid or solid at its standard state is constant and equal to 1.
of a pure liquid or solid at its standard state is constant and equal to 1. ![]() is not pure as there are solutes in it, however, the approximate model assumes water activity is not affected by the solutes, hence its activity is also equal to 1. Thus
is not pure as there are solutes in it, however, the approximate model assumes water activity is not affected by the solutes, hence its activity is also equal to 1. Thus
![]()
As a result, the expression for Q becomes
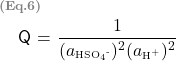
Using the approximate model, the solute activity is assumed to be equal to its concentration, in this case, its molality. Although, at 3 molal (high concentration), this assumption is not valid, however, for demonstration purposes, we will go ahead with the calculation
![]()
and
![]()
hence, Eq.6 becomes
![]()
or ![]() Q
Q ![]() 0.01235
0.01235
Therefore,
![]()
or
E![]() +1.98 V (rounded to 2 decimal places), and E
+1.98 V (rounded to 2 decimal places), and E![]() 1.98
1.98 ![]() 6
6 ![]() +11.86 V
+11.86 V
Using data digitized from Treptow, a combined graph can be generated for comparison of results calculated from the two models (the rigorous model and the approximate model) and those actually measured from a typical lead-acid cell (see Figure 2).
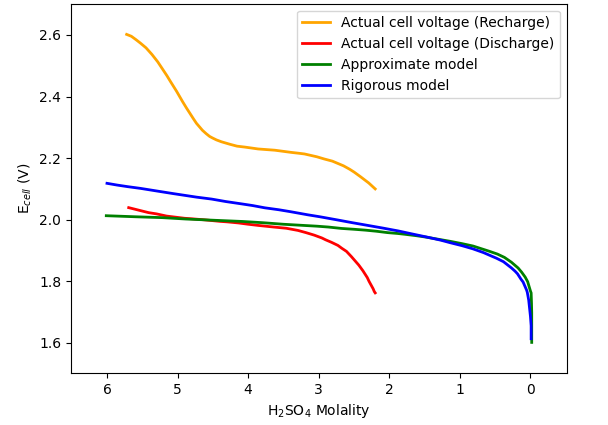
Figure 2:
Recharge and discharge potentials of a lead-acid cell versus sulfuric acid concentration. Data were digitized from Treptow [Treptow, R.S., 2002].
Note that, the actual (measured) discharge voltage is lower than the true cell voltage Ecell because of energy loss due to cell polarization effects; on the other hand, the recharge voltage is higher than the true Ecell as more energy is needed to overcome the polarization effects. It could be said that the true Ecell lies in the middle region between the actual discharge and the recharge curves.
This post was written based on following sources:
Atkins, P.W.; Physical Chemistry, Oxford University Press, 6th Ed., New York
https://openstax.org/details/books/chemistry-2e, ch 17, 905–915
Pavlov, D.; Kirchev, A.; Stoycheva, M.; Monahov, B.; Influence of H2SO4 concentration on the mechanism of the processes and on the electrochemical activity of the Pb/PbO2/PbSO4 electrode, J. Power Sources 2004, 137, 288–308
Staples B. R., Activity and Osmotic Coefficients of Aqueous Sulfuric Acid at 298.15 K, J. Phys. Chem. Ref. Data 1981, Vol. 10, No.3,
Treptow, R. S.; The Lead-Acid Battery: Its Voltage in Theory and in Practice, J. Chem. Educ. 2002, 79, 3, 334-338
Varela, F. E.; Codaro, E. N.; Vilche, J. R.; Reaction and system modelling for Pb and PbO2 electrodes; J. Appl. Electrochem., 1997, 27, 1232–1244
