Finding the Cartesian equation of a line in the complex plane
Question
Find the Cartesian form in the complex plane for the following equations, given ![]() ,
,
(a) ![]()
(b) ![]()
Answer
Note that the Cartesian form of a complex number ![]() is
is ![]() , where
, where ![]() is called an
is called an ![]() , and
, and ![]() , and the absolute
, and the absolute ![]() , also called the modulus of
, also called the modulus of ![]() , is defined as
, is defined as ![]() . Thus solutions to the above problems are as follows
. Thus solutions to the above problems are as follows
(a) ![]() ,
, ![]() :
:
Let ![]() , substituting
, substituting ![]() in
in ![]() , we get
, we get
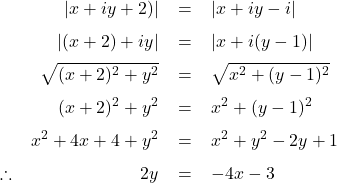
![]()
This is the Cartesian equation of a straight line with a gradient of ![]() and a y-intercept of
and a y-intercept of ![]() (see Figure 1)
(see Figure 1)
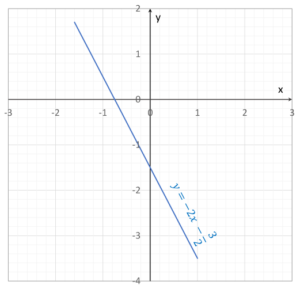
Figure 1
(b) ![]() ,
, ![]() :
:
Let ![]() , substituting
, substituting ![]() in
in ![]() , we get
, we get
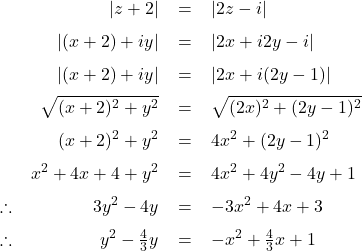
Completing the square gives
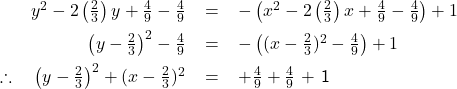
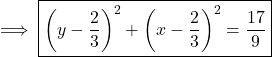
This is the Cartesian equation of a circle with the center at ![]() and a radius of
and a radius of ![]() (see Figure 2)
(see Figure 2)
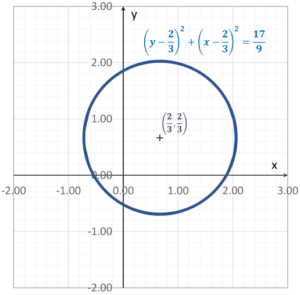
Figure 2
