Number Systems

The concept of number systems (or numbering systems) and the process of converting a number from one base to another via the decimal number system were explained in Number Systems and Their Decimal Equivalents and Decimal Number Conversion to Other Number Systems. On this page, we will explore the relationship between binary numbers and quaternary, octal, and hexadecimal numbers, and describe a simpler method for converting these numbers to binary and vice versa.

A. Quaternary, Octal and Hexadecimal Numbers to Binary

Quaternary numbers (Base-4)

Substituting 4 = 2² in Eq. A.1, we get

In the binary number system, numbers 0, 1, 2, and 3 are represented as

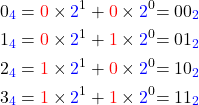
Thus Eq. A.2 can be written as

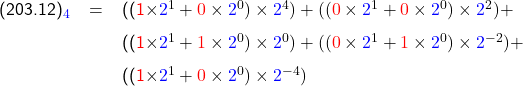
or

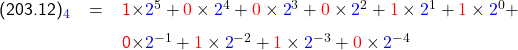
or

Comparing Eqs. A.1, A.3, and A.4b, it can be concluded that to convert a quaternary number to a binary number, we can simply replace each quaternary digit with its equivalent 2-bit binary. Matching color for each quaternary digit and its equivalent 2-bit binary number in Eq. A.4c is used to demonstrate this conversion approach as shown below (note that the binary number 110011.0110 can be expressed as 110011.011)

Octal numbers (Base-8)

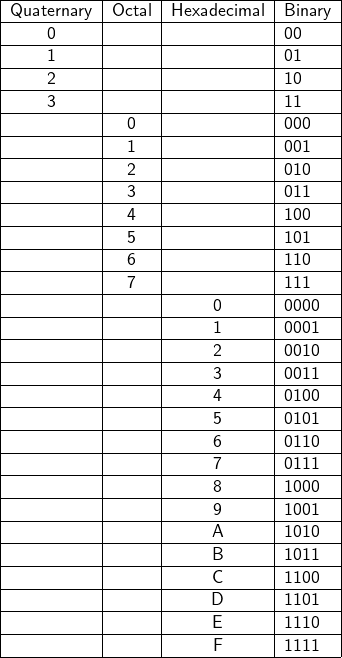
A similar method can be used for conversion of octal numbers to binary numbers, except that, as the base of an octal number is 8, which is 2³, an octal digit must be replaced with a 3-bit binary number instead of 2-bit. 3-bit binary number for each of eight octal digits can be derived in the same way as that of Eq. A.3; and similarly 4-bit binary numbers for 16 hexadecimal digits. 2-bit, 3-bit, and 4-bit binary numbers for each of quaternary, octal, and hexadecimal digits are shown in Table A.1 below.

For example, conversion of octal number 72 to binary:

Converting octal number 72.03 to binary:

Hexadecimal numbers (Base-16)

Similarly, to convert a hexadecimal number to binary number, note that hexadecimal number has a base of 16, which is 2⁴, so a 4-bit binary number will be used to replace each hexadecimal digit.

For example, to convert hexadecimal number A1E to binary number, we substitute A, 1, and B with their respective 4-bit binary number as below

and converting hexadecimal number A1E.2D to binary number can be done in a similar fashion:

---

B. Binary Numbers to Quaternary, Octal or Hexadecimal

Conversion of a binary number to quaternary, or octal, or hexadecimal number is the reverse of the above process with 2-bit binary for quaternary, 3-bit for octal, and 4-bit for hexadecimal. Also, for the whole number part, the replacement starts from right to left, and padding of zeros may be needed to the last left digit to make up for its respective bit size. For the fractional part, if any, the replacement starts from the fractional point and from left to right, and padding of zeros may be needed to the last right digit to make up for the respective bit size.

Quaternary Numbers

To convert a binary number, says 1011, to quaternary, we start with substituting the last two digits, 11, with 3 , then binary digits 10 with 2 and adding it to the left of 3 to make quaternary number 23.

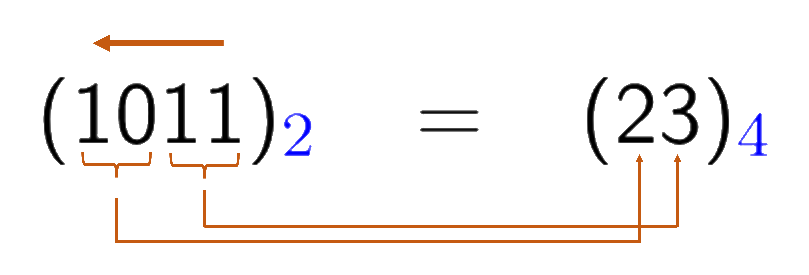
To convert binary number 11011, after replacing 11 with 3 and 10 with 2, a zero is padded to the left of the remaining binary digit 1 to make a 2-bit binary 01, which is 1 in quaternary system. The quaternary result is 123, and the padded zero is highlighted in red as shown below,

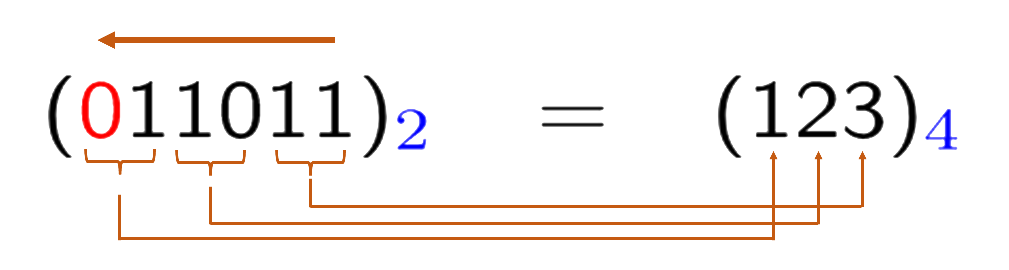
To convert binary number 11011.011 to quaternary number, the whole number (before the fractional point) is equal to quaternary 123, as explained earlier. For the fractional part, we start with 01, the first two digits immediately on the right of the fractional point, which has quaternary value of 1 (see Table A.1); we then add a zero to the right of the remaining 1 to make 2-bit binary 10. The resulted quaternary number is shown below, padded zeros are in red color for the whole number part and green for the fractional part.

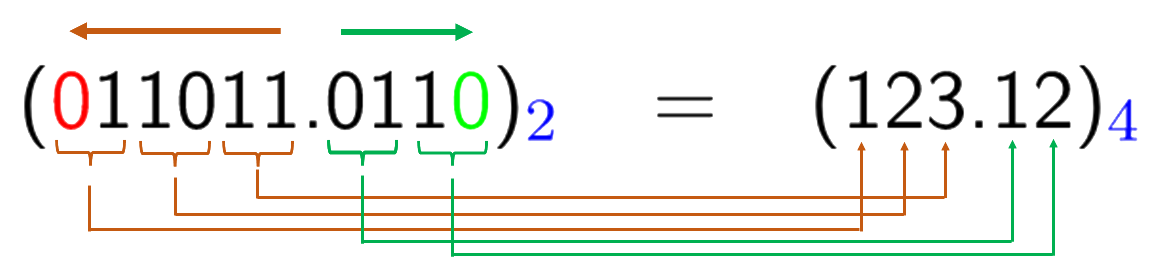
Octal numbers

To convert binary number 1011 to octal, similar steps can be used but with 3-bit binary.

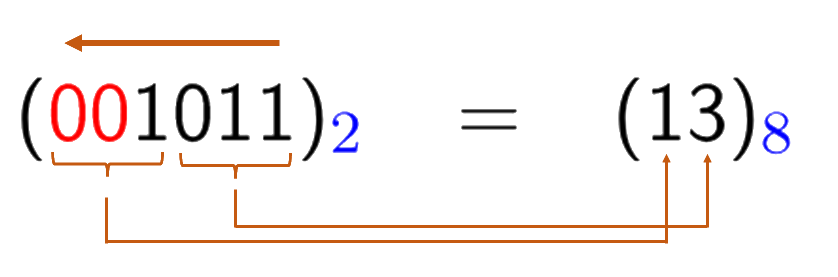
Convert binary 11011.011 to octal number:

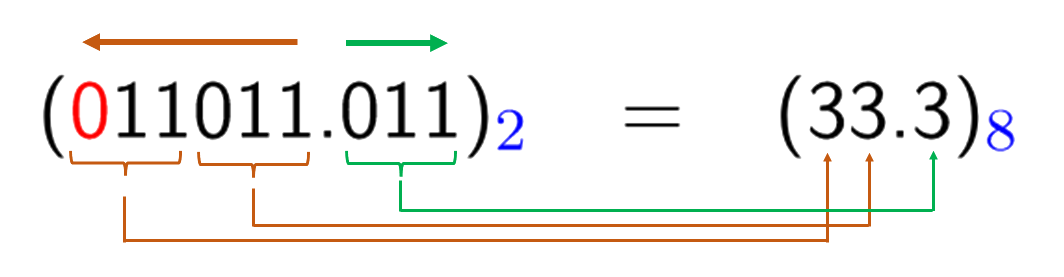
Hexadecimal Numbers

Converting binary number 1011 to hexadecimal number

Converting binary number 11011.011 to hexadecimal number

---

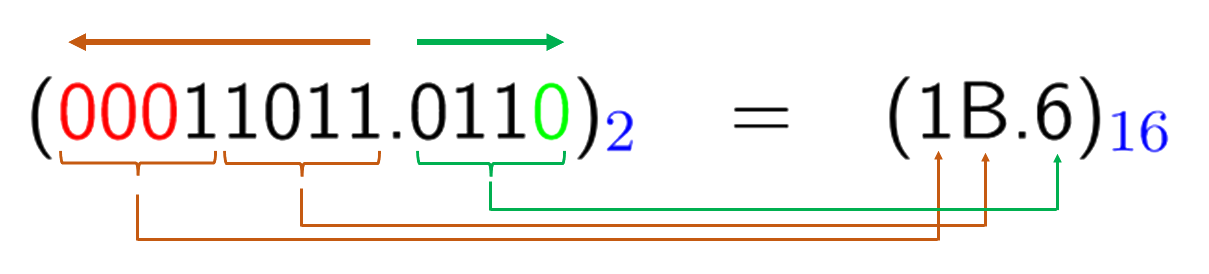
Binary Equivalents of Quaternary, Octal and Hexadecimal Numbers

Binary equivalents of quaternary, octal and hexadecimal numbers

---

Number Systems and Their Decimal Equivalents

Decimal Numbers – Conversion to Other Number Systems

Number Conversion Tool