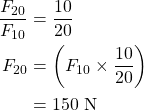Calculating velocity from a Force-Time graph
PROBLEM:
A force F acts on a stationary object of a mass of 96 g for a duration of 30 milliseconds, causing it to move away from its initial position in a straight line on a frictionless surface. Fig. 1 shows the force as a function of time during that 30 milliseconds. Calculate the velocity of the object at times t = 5 ms, 20 ms, and 35 ms.
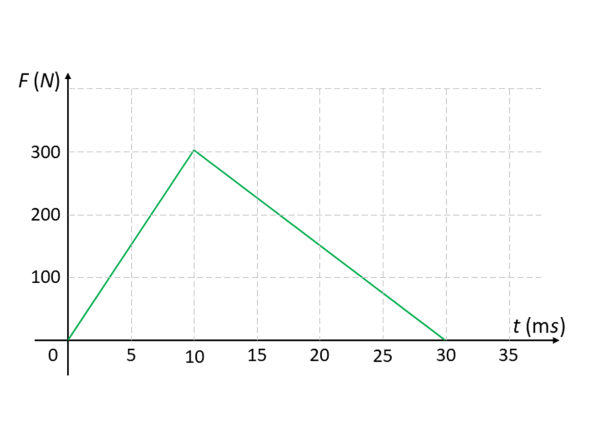
Fig. 1
SOLUTION:
Let ![]() be the mass of the object, and
be the mass of the object, and ![]() ,
, ![]() ,
, ![]() ,
, ![]() be its velocity at time
be its velocity at time ![]() 0 s, 5 s, 20 s, 35 s, respectively.
0 s, 5 s, 20 s, 35 s, respectively.
The force ![]() that acts on the object during time
that acts on the object during time ![]() provides the object with an impulse of
provides the object with an impulse of ![]() and change its momentum from
and change its momentum from ![]() to
to ![]() . According to the impulse-momentum theorem,
. According to the impulse-momentum theorem, ![]() , we have:
, we have:
![]()
As the object moves in a straight line, we can use this line as ![]() -axis with forward direction as positive, and make it an one dimensional motion. As a result, all quantities can be handled as scalars to simplify our calculations. Also, as force
-axis with forward direction as positive, and make it an one dimensional motion. As a result, all quantities can be handled as scalars to simplify our calculations. Also, as force ![]() changes with time, it is more appropriate to use differentiation notion for impulse and momentum:
changes with time, it is more appropriate to use differentiation notion for impulse and momentum:
![]()
where ![]() is the impulse on the object during the period of time
is the impulse on the object during the period of time ![]() that causes its velocity to change an amount of
that causes its velocity to change an amount of ![]() . Velocity
. Velocity ![]() at time
at time ![]() can be calculated by integrating both sides of Eq. (2). Note that
can be calculated by integrating both sides of Eq. (2). Note that ![]() 0 as the object is stationary at start; also note that
0 as the object is stationary at start; also note that ![]() is the area underneath the line
is the area underneath the line ![]() , encapsulated by lines
, encapsulated by lines ![]() 0,
0, ![]() ,
, ![]() , and
, and ![]() .
.
Calculations
![]()
Using SI units, ![]() , and
, and ![]() ,
, ![]() ,
,![]() ,
, ![]() 0 s, 0.005 s, 0.020 s, 0.035 s, respectively. Magnitude of force
0 s, 0.005 s, 0.020 s, 0.035 s, respectively. Magnitude of force ![]() at
at ![]() ,
, ![]() ,
,![]() , and
, and ![]() are
are ![]() ,
, ![]() ,
,![]() , and
, and ![]() , respectively.
, respectively.
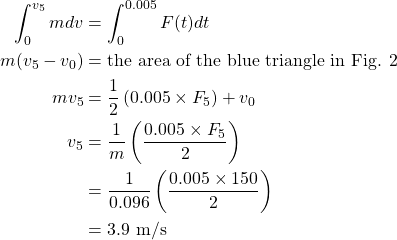
Value of ![]() is obtained as explained in the “Notes” Section below.
is obtained as explained in the “Notes” Section below.
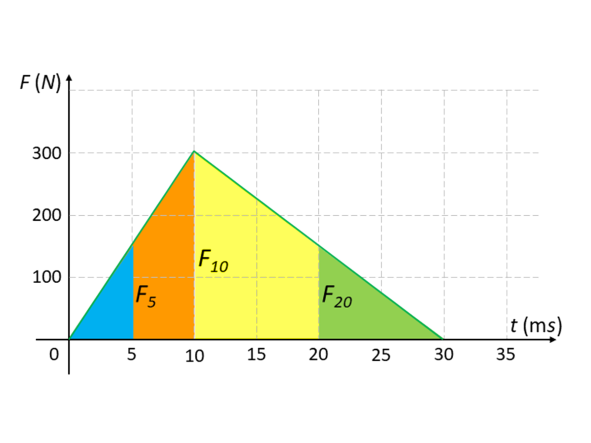
Fig. 2
![]()

![]()
After 0.030 seconds, there is no force acting on the object, therefore it continues to travel with constant speed ![]() , that is,
, that is, ![]() , and
, and ![]() can be calculated as follows
can be calculated as follows
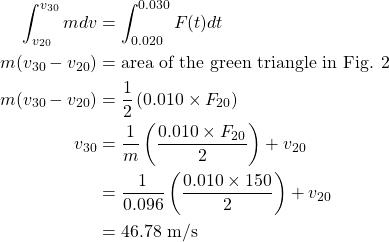
![]()
As shown in Fig. 1, ![]() 300 N.
300 N. ![]() and
and ![]() can be calculated using triangle similarity rules. As the blue triangle and the triangle made up by blue triangle and orange trapezoid are similar, we have
can be calculated using triangle similarity rules. As the blue triangle and the triangle made up by blue triangle and orange trapezoid are similar, we have
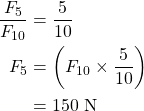
Similarly, the green triangle and the triangle made up by green triangle and yellow trapezoid are similar, therefore